A Few Moments Please: Scalable Graphon Learning via Moment Matching

Graphons, as limit objects of dense graph sequences, play a central role in the statistical analysis of network data. However, existing graphon estimation methods often struggle with scalability to large networks and resolution-independent approximation, due to their reliance on estimating latent variables or costly metrics such as the Gromov-Wasserstein distance. In this work, we propose a novel, scalable graphon estimator that directly recovers the graphon via moment matching, leveraging implicit neural representations (INRs). Our approach avoids latent variable modeling by training an INR--mapping coordinates to graphon values--to match empirical subgraph counts (i.e., moments) from observed graphs. This direct estimation mechanism yields a polynomial-time solution and crucially sidesteps the combinatorial complexity of Gromov-Wasserstein optimization. Building on foundational results, we establish a theoretical guarantee: when the observed subgraph motifs sufficiently represent those of the true graphon (a condition met with sufficiently large or numerous graph samples), the estimated graphon achieves a provable upper bound in cut distance from the ground truth. Additionally, we introduce MomentMixup, a data augmentation technique that performs mixup in the moment space to enhance graphon-based learning. Our graphon estimation method achieves strong empirical performance--demonstrating high accuracy on small graphs and superior computational efficiency on large graphs--outperforming state-of-the-art scalable estimators in 75\% of benchmark settings and matching them in the remaining cases. Furthermore, MomentMixup demonstrated improved graph classification accuracy on the majority of our benchmarks.

Graph Guided Diffusion: Unified Guidance for Conditional Graph Generation

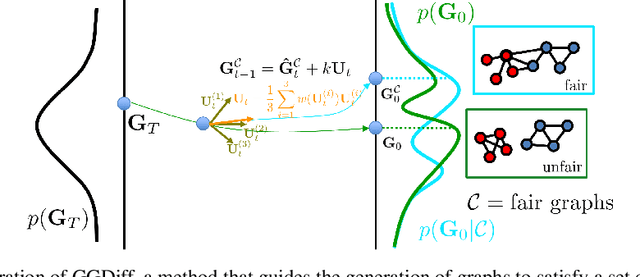
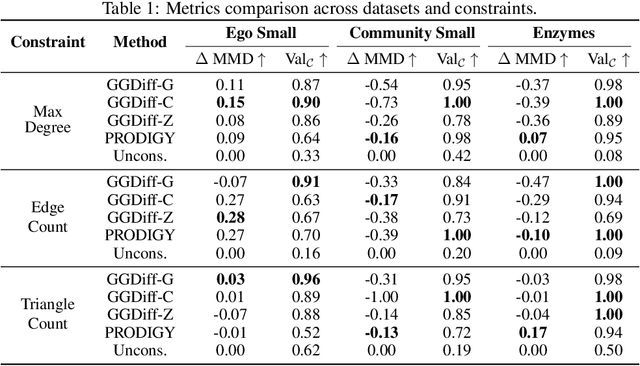
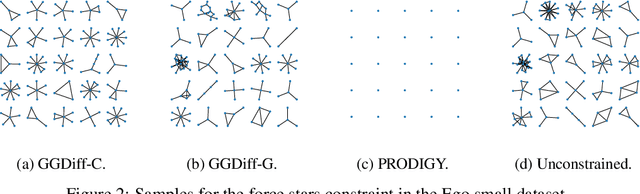
Diffusion models have emerged as powerful generative models for graph generation, yet their use for conditional graph generation remains a fundamental challenge. In particular, guiding diffusion models on graphs under arbitrary reward signals is difficult: gradient-based methods, while powerful, are often unsuitable due to the discrete and combinatorial nature of graphs, and non-differentiable rewards further complicate gradient-based guidance. We propose Graph Guided Diffusion (GGDiff), a novel guidance framework that interprets conditional diffusion on graphs as a stochastic control problem to address this challenge. GGDiff unifies multiple guidance strategies, including gradient-based guidance (for differentiable rewards), control-based guidance (using control signals from forward reward evaluations), and zero-order approximations (bridging gradient-based and gradient-free optimization). This comprehensive, plug-and-play framework enables zero-shot guidance of pre-trained diffusion models under both differentiable and non-differentiable reward functions, adapting well-established guidance techniques to graph generation--a direction largely unexplored. Our formulation balances computational efficiency, reward alignment, and sample quality, enabling practical conditional generation across diverse reward types. We demonstrate the efficacy of GGDiff in various tasks, including constraints on graph motifs, fairness, and link prediction, achieving superior alignment with target rewards while maintaining diversity and fidelity.

Matched Topological Subspace Detector

Topological spaces, represented by simplicial complexes, capture richer relationships than graphs by modeling interactions not only between nodes but also among higher-order entities, such as edges or triangles. This motivates the representation of information defined in irregular domains as topological signals. By leveraging the spectral dualities of Hodge and Dirac theory, practical topological signals often concentrate in specific spectral subspaces (e.g., gradient or curl). For instance, in a foreign currency exchange network, the exchange flow signals typically satisfy the arbitrage-free condition and hence are curl-free. However, the presence of anomalies can disrupt these conditions, causing the signals to deviate from such subspaces. In this work, we formulate a hypothesis testing framework to detect whether simplicial complex signals lie in specific subspaces in a principled and tractable manner. Concretely, we propose Neyman-Pearson matched topological subspace detectors for signals defined at a single simplicial level (such as edges) or jointly across all levels of a simplicial complex. The (energy-based projection) proposed detectors handle missing values, provide closed-form performance analysis, and effectively capture the unique topological properties of the data. We demonstrate the effectiveness of the proposed topological detectors on various real-world data, including foreign currency exchange networks.

Structure-Guided Input Graph for GNNs facing Heterophily

Graph Neural Networks (GNNs) have emerged as a promising tool to handle data exhibiting an irregular structure. However, most GNN architectures perform well on homophilic datasets, where the labels of neighboring nodes are likely to be the same. In recent years, an increasing body of work has been devoted to the development of GNN architectures for heterophilic datasets, where labels do not exhibit this low-pass behavior. In this work, we create a new graph in which nodes are connected if they share structural characteristics, meaning a higher chance of sharing their labels, and then use this new graph in the GNN architecture. To do this, we compute the k-nearest neighbors graph according to distances between structural features, which are either (i) role-based, such as degree, or (ii) global, such as centrality measures. Experiments show that the labels are smoother in this newly defined graph and that the performance of GNN architectures improves when using this alternative structure.

Exploiting the Structure of Two Graphs with Graph Neural Networks

Graph neural networks (GNNs) have emerged as a promising solution to deal with unstructured data, outperforming traditional deep learning architectures. However, most of the current GNN models are designed to work with a single graph, which limits their applicability in many real-world scenarios where multiple graphs may be involved. To address this limitation, we propose a novel graph-based deep learning architecture to handle tasks where two sets of signals exist, each defined on a different graph. First we consider the setting where the input is represented as a signal on top of one graph (input graph) and the output is a graph signal defined over a different graph (output graph). For this setup, we propose a three-block architecture where we first process the input data using a GNN that operates over the input graph, then apply a transformation function that operates in a latent space and maps the signals from the input to the output graph, and finally implement a second GNN that operates over the output graph. Our goal is not to propose a single specific definition for each of the three blocks, but rather to provide a flexible approach to solve tasks involving data defined on two graphs. The second part of the paper addresses a self-supervised setup, where the focus is not on the output space but on the underlying latent space and, inspired by Canonical Correlation Analysis, we seek informative representations of the data that can be leveraged to solve a downstream task. By leveraging information from multiple graphs, the proposed architecture can capture more intricate relationships between different entities in the data. We test this in several experimental setups using synthetic and real world datasets, and observe that the proposed architecture works better than traditional deep learning architectures, showcasing the importance of leveraging the information of the two graphs.

Redesigning graph filter-based GNNs to relax the homophily assumption

Graph neural networks (GNNs) have become a workhorse approach for learning from data defined over irregular domains, typically by implicitly assuming that the data structure is represented by a homophilic graph. However, recent works have revealed that many relevant applications involve heterophilic data where the performance of GNNs can be notably compromised. To address this challenge, we present a simple yet effective architecture designed to mitigate the limitations of the homophily assumption. The proposed architecture reinterprets the role of graph filters in convolutional GNNs, resulting in a more general architecture while incorporating a stronger inductive bias than GNNs based on filter banks. The proposed convolutional layer enhances the expressive capacity of the architecture enabling it to learn from both homophilic and heterophilic data and preventing the issue of oversmoothing. From a theoretical standpoint, we show that the proposed architecture is permutation equivariant. Finally, we show that the proposed GNNs compares favorably relative to several state-of-the-art baselines in both homophilic and heterophilic datasets, showcasing its promising potential.

Tracking Network Dynamics using Probabilistic State-Space Models

This paper introduces a probabilistic approach for tracking the dynamics of unweighted and directed graphs using state-space models (SSMs). Unlike conventional topology inference methods that assume static graphs and generate point-wise estimates, our method accounts for dynamic changes in the network structure over time. We model the network at each timestep as the state of the SSM, and use observations to update beliefs that quantify the probability of the network being in a particular state. Then, by considering the dynamics of transition and observation models through the update and prediction steps, respectively, the proposed method can incorporate the information of real-time graph signals into the beliefs. These beliefs provide a probability distribution of the network at each timestep, being able to provide both an estimate for the network and the uncertainty it entails. Our approach is evaluated through experiments with synthetic and real-world networks. The results demonstrate that our method effectively estimates network states and accounts for the uncertainty in the data, outperforming traditional techniques such as recursive least squares.

A Primal-Dual-Assisted Penalty Approach to Bilevel Optimization with Coupled Constraints

Interest in bilevel optimization has grown in recent years, partially due to its applications to tackle challenging machine-learning problems. Several exciting recent works have been centered around developing efficient gradient-based algorithms that can solve bilevel optimization problems with provable guarantees. However, the existing literature mainly focuses on bilevel problems either without constraints, or featuring only simple constraints that do not couple variables across the upper and lower levels, excluding a range of complex applications. Our paper studies this challenging but less explored scenario and develops a (fully) first-order algorithm, which we term BLOCC, to tackle BiLevel Optimization problems with Coupled Constraints. We establish rigorous convergence theory for the proposed algorithm and demonstrate its effectiveness on two well-known real-world applications - hyperparameter selection in support vector machine (SVM) and infrastructure planning in transportation networks using the real data from the city of Seville.

Robust Graph Neural Network based on Graph Denoising

Graph Neural Networks (GNNs) have emerged as a notorious alternative to address learning problems dealing with non-Euclidean datasets. However, although most works assume that the graph is perfectly known, the observed topology is prone to errors stemming from observational noise, graph-learning limitations, or adversarial attacks. If ignored, these perturbations may drastically hinder the performance of GNNs. To address this limitation, this work proposes a robust implementation of GNNs that explicitly accounts for the presence of perturbations in the observed topology. For any task involving GNNs, our core idea is to i) solve an optimization problem not only over the learnable parameters of the GNN but also over the true graph, and ii) augment the fitting cost with a term accounting for discrepancies on the graph. Specifically, we consider a convolutional GNN based on graph filters and follow an alternating optimization approach to handle the (non-differentiable and constrained) optimization problem by combining gradient descent and projected proximal updates. The resulting algorithm is not limited to a particular type of graph and is amenable to incorporating prior information about the perturbations. Finally, we assess the performance of the proposed method through several numerical experiments.

Recovering Missing Node Features with Local Structure-based Embeddings

Node features bolster graph-based learning when exploited jointly with network structure. However, a lack of nodal attributes is prevalent in graph data. We present a framework to recover completely missing node features for a set of graphs, where we only know the signals of a subset of graphs. Our approach incorporates prior information from both graph topology and existing nodal values. We demonstrate an example implementation of our framework where we assume that node features depend on local graph structure. Missing nodal values are estimated by aggregating known features from the most similar nodes. Similarity is measured through a node embedding space that preserves local topological features, which we train using a Graph AutoEncoder. We empirically show not only the accuracy of our feature estimation approach but also its value for downstream graph classification. Our success embarks on and implies the need to emphasize the relationship between node features and graph structure in graph-based learning.