Domain Adaptive Unfolded Graph Neural Networks

Over the last decade, graph neural networks (GNNs) have made significant progress in numerous graph machine learning tasks. In real-world applications, where domain shifts occur and labels are often unavailable for a new target domain, graph domain adaptation (GDA) approaches have been proposed to facilitate knowledge transfer from the source domain to the target domain. Previous efforts in tackling distribution shifts across domains have mainly focused on aligning the node embedding distributions generated by the GNNs in the source and target domains. However, as the core part of GDA approaches, the impact of the underlying GNN architecture has received limited attention. In this work, we explore this orthogonal direction, i.e., how to facilitate GDA with architectural enhancement. In particular, we consider a class of GNNs that are designed explicitly based on optimization problems, namely unfolded GNNs (UGNNs), whose training process can be represented as bi-level optimization. Empirical and theoretical analyses demonstrate that when transferring from the source domain to the target domain, the lower-level objective value generated by the UGNNs significantly increases, resulting in an increase in the upper-level objective as well. Motivated by this observation, we propose a simple yet effective strategy called cascaded propagation (CP), which is guaranteed to decrease the lower-level objective value. The CP strategy is widely applicable to general UGNNs, and we evaluate its efficacy with three representative UGNN architectures. Extensive experiments on five real-world datasets demonstrate that the UGNNs integrated with CP outperform state-of-the-art GDA baselines.

Algorithm-Informed Graph Neural Networks for Leakage Detection and Localization in Water Distribution Networks

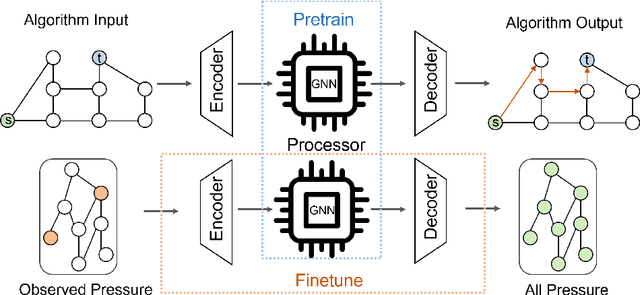
Detecting and localizing leakages is a significant challenge for the efficient and sustainable management of water distribution networks (WDN). Leveraging the inherent graph structure of WDNs, recent approaches have used graph-based data-driven methods. However, these methods often learn shortcuts that work well with in-distribution data but fail to generalize to out-of-distribution data. To address this limitation and inspired by the perfect generalization ability of classical algorithms, we propose an algorithm-informed graph neural network (AIGNN). Recognizing that WDNs function as flow networks, incorporating max-flow information can be beneficial for inferring pressures. In the proposed framework, we first train AIGNN to emulate the Ford-Fulkerson algorithm for solving max-flow problems. This algorithmic knowledge is then transferred to address the pressure estimation problem in WDNs. Two AIGNNs are deployed, one to reconstruct pressure based on the current measurements, and another to predict pressure based on previous measurements. Leakages are detected and localized by comparing the outputs of the reconstructor and the predictor. By pretraining AIGNNs to reason like algorithms, they are expected to extract more task-relevant and generalizable features. Experimental results demonstrate that the proposed algorithm-informed approach achieves superior results with better generalization ability compared to GNNs that do not incorporate algorithmic knowledge.

Discerning and Enhancing the Weighted Sum-Rate Maximization Algorithms in Communications

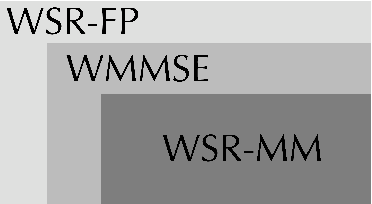
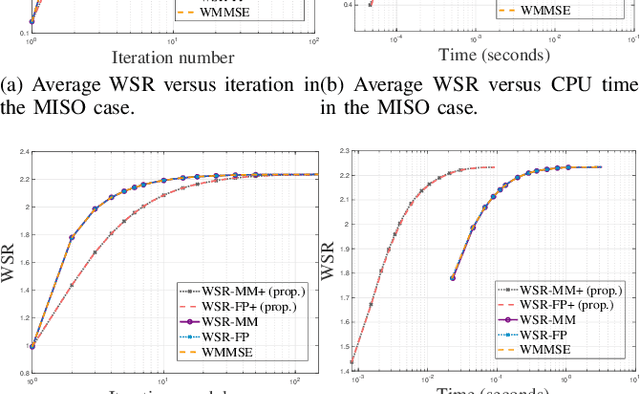
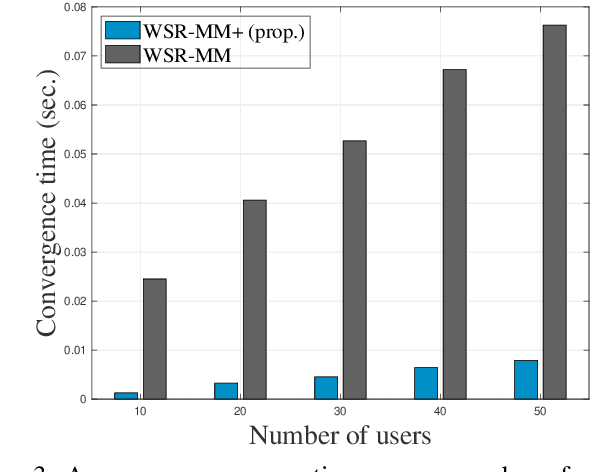
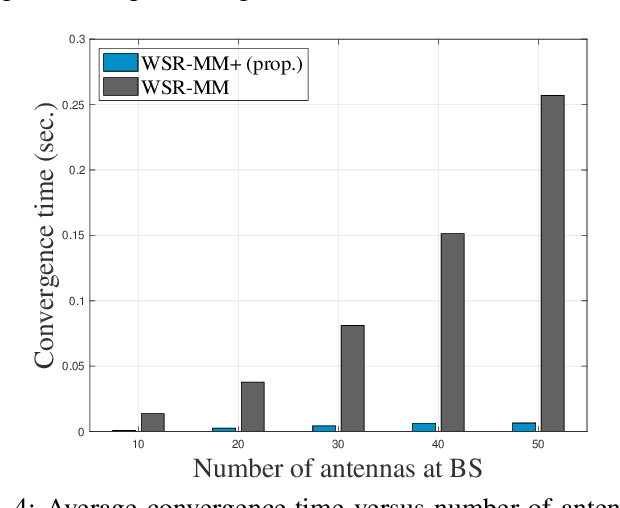
Weighted sum-rate (WSR) maximization plays a critical role in communication system design. This paper examines three optimization methods for WSR maximization, which ensure convergence to stationary points: two block coordinate ascent (BCA) algorithms, namely, weighted sum-minimum mean-square error (WMMSE) and WSR maximization via fractional programming (WSR-FP), along with a minorization-maximization (MM) algorithm, WSR maximization via MM (WSR-MM). Our contributions are threefold. Firstly, we delineate the exact relationships among WMMSE, WSR-FP, and WSR-MM, which, despite their extensive use in the literature, lack a comprehensive comparative study. By probing the theoretical underpinnings linking the BCA and MM algorithmic frameworks, we reveal the direct correlations between the equivalent transformation techniques, essential to the development of WMMSE and WSR-FP, and the surrogate functions pivotal to WSR-MM. Secondly, we propose a novel algorithm, WSR-MM+, harnessing the flexibility of selecting surrogate functions in MM framework. By circumventing the repeated matrix inversions in the search for optimal Lagrange multipliers in existing algorithms, WSR-MM+ significantly reduces the computational load per iteration and accelerates convergence. Thirdly, we reconceptualize WSR-MM+ within the BCA framework, introducing a new equivalent transform, which gives rise to an enhanced version of WSR-FP, named as WSR-FP+. We further demonstrate that WSR-MM+ can be construed as the basic gradient projection method. This perspective yields a deeper understanding into its computational intricacies. Numerical simulations corroborate the connections between WMMSE, WSR-FP, and WSR-MM and confirm the efficacy of the proposed WSR-MM+ and WSR-FP+ algorithms.

ASGNN: Graph Neural Networks with Adaptive Structure

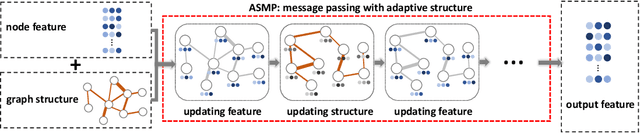
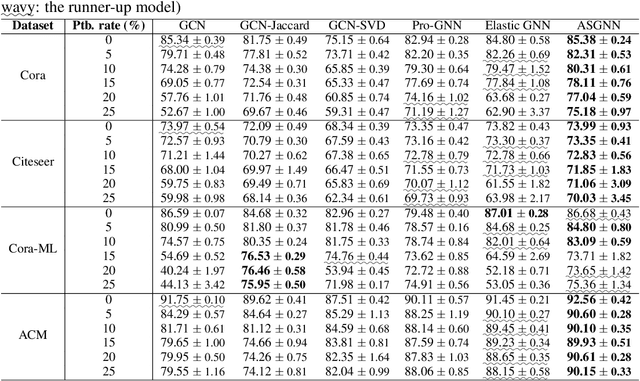
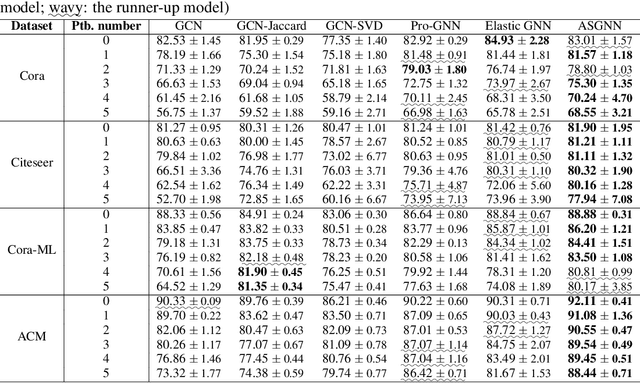
The graph neural network (GNN) models have presented impressive achievements in numerous machine learning tasks. However, many existing GNN models are shown to be vulnerable to adversarial attacks, which creates a stringent need to build robust GNN architectures. In this work, we propose a novel interpretable message passing scheme with adaptive structure (ASMP) to defend against adversarial attacks on graph structure. Layers in ASMP are derived based on optimization steps that minimize an objective function that learns the node feature and the graph structure simultaneously. ASMP is adaptive in the sense that the message passing process in different layers is able to be carried out over dynamically adjusted graphs. Such property allows more fine-grained handling of the noisy (or perturbed) graph structure and hence improves the robustness. Convergence properties of the ASMP scheme are theoretically established. Integrating ASMP with neural networks can lead to a new family of GNN models with adaptive structure (ASGNN). Extensive experiments on semi-supervised node classification tasks demonstrate that the proposed ASGNN outperforms the state-of-the-art GNN architectures in terms of classification performance under various adversarial attacks.

Towards Understanding Graph Neural Networks: An Algorithm Unrolling Perspective

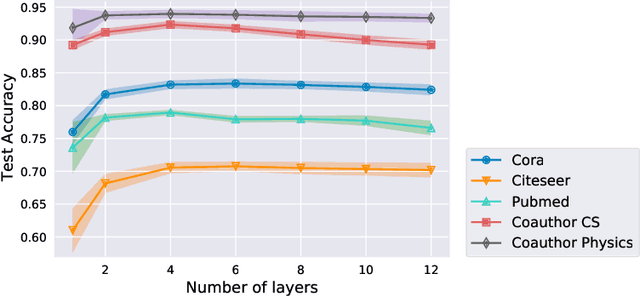
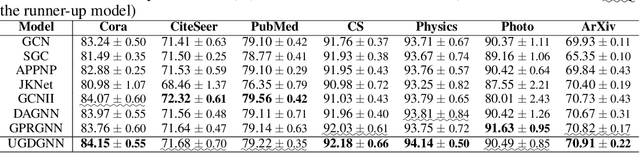
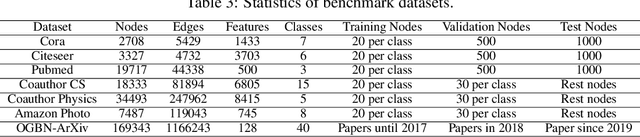
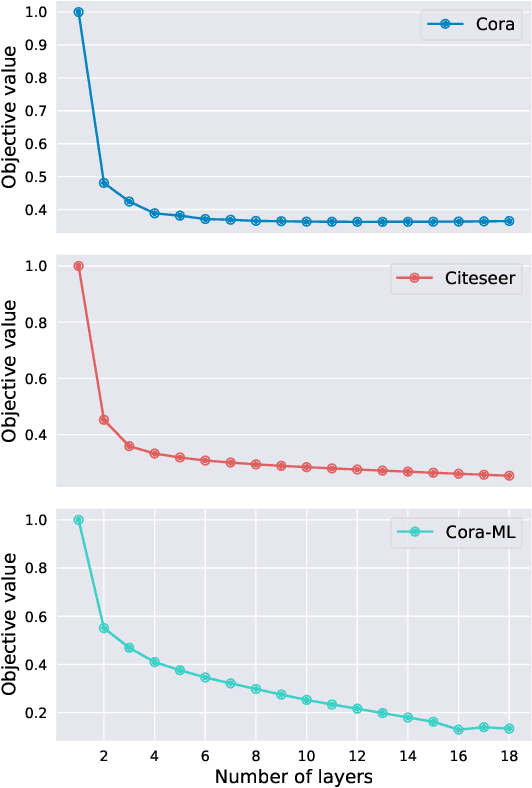
The graph neural network (GNN) has demonstrated its superior performance in various applications. The working mechanism behind it, however, remains mysterious. GNN models are designed to learn effective representations for graph-structured data, which intrinsically coincides with the principle of graph signal denoising (GSD). Algorithm unrolling, a "learning to optimize" technique, has gained increasing attention due to its prospects in building efficient and interpretable neural network architectures. In this paper, we introduce a class of unrolled networks built based on truncated optimization algorithms (e.g., gradient descent and proximal gradient descent) for GSD problems. They are shown to be tightly connected to many popular GNN models in that the forward propagations in these GNNs are in fact unrolled networks serving specific GSDs. Besides, the training process of a GNN model can be seen as solving a bilevel optimization problem with a GSD problem at the lower level. Such a connection brings a fresh view of GNNs, as we could try to understand their practical capabilities from their GSD counterparts, and it can also motivate designing new GNN models. Based on the algorithm unrolling perspective, an expressive model named UGDGNN, i.e., unrolled gradient descent GNN, is further proposed which inherits appealing theoretical properties. Extensive numerical simulations on seven benchmark datasets demonstrate that UGDGNN can achieve superior or competitive performance over the state-of-the-art models.

Weighted Sum-Rate Maximization for Multi-Hop RIS-Aided Multi-User Communications: A Minorization-Maximization Approach

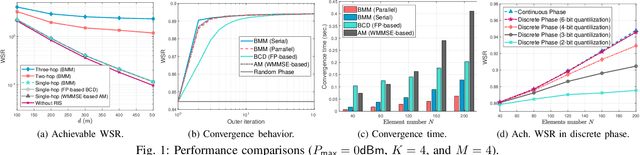
The reconfigurable intelligent surface (RIS) has aroused much research attention recently due to its potential benefits in 5G and beyond wireless networks. This paper considers a general multi-hop RIS-aided multi-user communication system and the weighted sum-rate maximization problem is studied by jointly designing the active beamforming matrix at the base station and multiple phase-shift matrices at the RISs (considering both continuous and discrete phase constraints). To tackle the resulting highly nonconvex optimization problem, a problem-tailored low-complexity and globally convergent algorithm based on block minorization-maximization (BMM) is proposed. The effectiveness of the proposed BMM approach and the performance improvement gained with multi-hop RISs are both demonstrated through numerical simulations. The merits of the proposed algorithms are further illustrated by indicating their adaptivity in solving many other RIS-related system designs.