Algorithm-Informed Graph Neural Networks for Leakage Detection and Localization in Water Distribution Networks
Paper and Code
Aug 05, 2024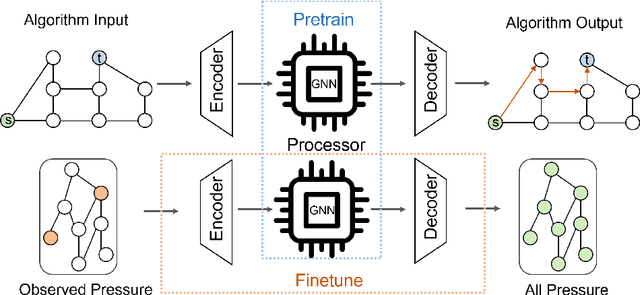



Detecting and localizing leakages is a significant challenge for the efficient and sustainable management of water distribution networks (WDN). Leveraging the inherent graph structure of WDNs, recent approaches have used graph-based data-driven methods. However, these methods often learn shortcuts that work well with in-distribution data but fail to generalize to out-of-distribution data. To address this limitation and inspired by the perfect generalization ability of classical algorithms, we propose an algorithm-informed graph neural network (AIGNN). Recognizing that WDNs function as flow networks, incorporating max-flow information can be beneficial for inferring pressures. In the proposed framework, we first train AIGNN to emulate the Ford-Fulkerson algorithm for solving max-flow problems. This algorithmic knowledge is then transferred to address the pressure estimation problem in WDNs. Two AIGNNs are deployed, one to reconstruct pressure based on the current measurements, and another to predict pressure based on previous measurements. Leakages are detected and localized by comparing the outputs of the reconstructor and the predictor. By pretraining AIGNNs to reason like algorithms, they are expected to extract more task-relevant and generalizable features. Experimental results demonstrate that the proposed algorithm-informed approach achieves superior results with better generalization ability compared to GNNs that do not incorporate algorithmic knowledge.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge