Elliptical Wishart distributions: information geometry, maximum likelihood estimator, performance analysis and statistical learning

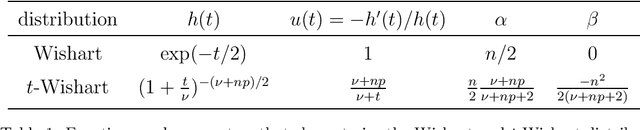
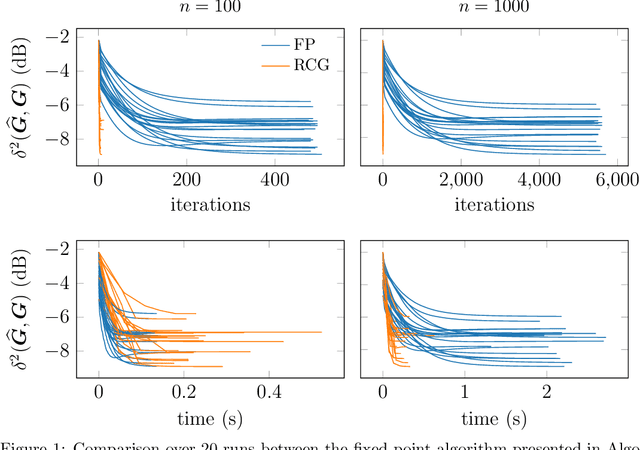
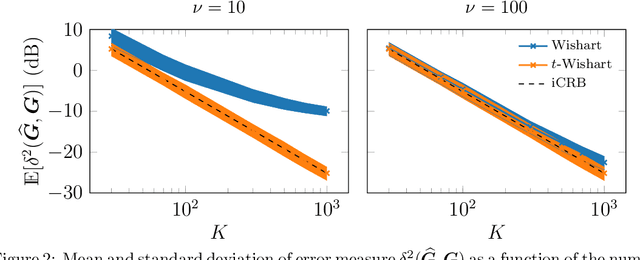
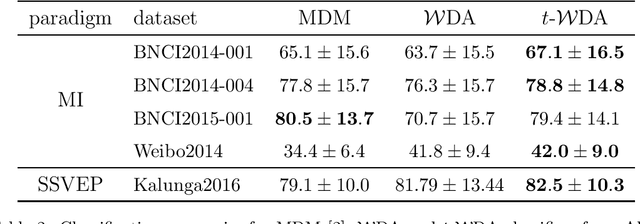
This paper deals with Elliptical Wishart distributions - which generalize the Wishart distribution - in the context of signal processing and machine learning. Two algorithms to compute the maximum likelihood estimator (MLE) are proposed: a fixed point algorithm and a Riemannian optimization method based on the derived information geometry of Elliptical Wishart distributions. The existence and uniqueness of the MLE are characterized as well as the convergence of both estimation algorithms. Statistical properties of the MLE are also investigated such as consistency, asymptotic normality and an intrinsic version of Fisher efficiency. On the statistical learning side, novel classification and clustering methods are designed. For the $t$-Wishart distribution, the performance of the MLE and statistical learning algorithms are evaluated on both simulated and real EEG and hyperspectral data, showcasing the interest of our proposed methods.

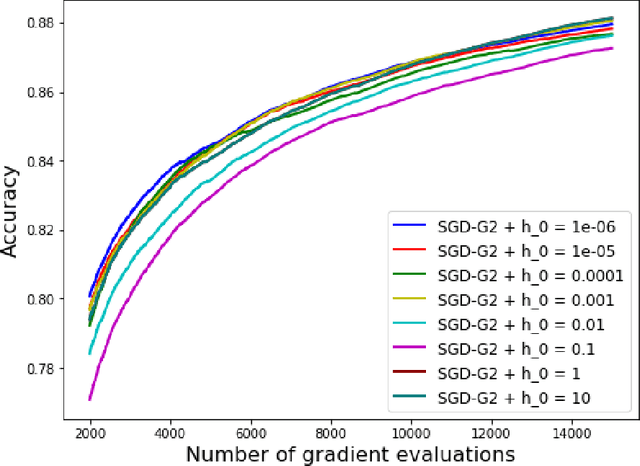
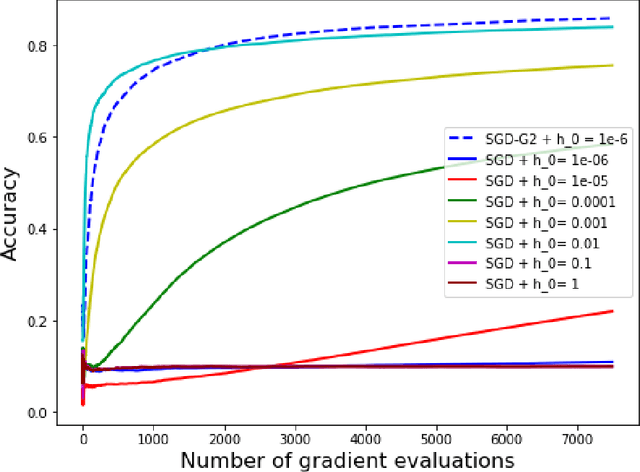
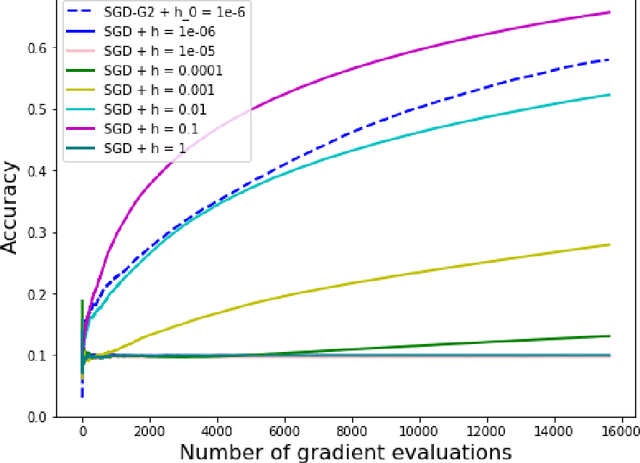
Stochastic Runge-Kutta methods and adaptive SGD-G2 stochastic gradient descent

The minimization of the loss function is of paramount importance in deep neural networks. On the other hand, many popular optimization algorithms have been shown to correspond to some evolution equation of gradient flow type. Inspired by the numerical schemes used for general evolution equations we introduce a second order stochastic Runge Kutta method and show that it yields a consistent procedure for the minimization of the loss function. In addition it can be coupled, in an adaptive framework, with a Stochastic Gradient Descent (SGD) to adjust automatically the learning rate of the SGD, without the need of any additional information on the Hessian of the loss functional. The adaptive SGD, called SGD-G2, is successfully tested on standard datasets.