Lyapunov weights to convey the meaning of time in physics-informed neural networks

Time is not a dimension as the others. In Physics-Informed Neural Networks (PINN) several proposals attempted to adapt the time sampling or time weighting to take into account the specifics of this special dimension. But these proposals are not principled and need guidance to be used. We explain here theoretically why the Lyapunov exponents give actionable insights and propose a weighting scheme to automatically adapt to chaotic, periodic or stable dynamics. We characterize theoretically the best weighting scheme under computational constraints as a cumulative exponential integral of the local Lyapunov exponent estimators and show that it performs well in practice under the regimes mentioned above.

Optimal time sampling in physics-informed neural networks

Physics-informed neural networks (PINN) is a extremely powerful paradigm used to solve equations encountered in scientific computing applications. An important part of the procedure is the minimization of the equation residual which includes, when the equation is time-dependent, a time sampling. It was argued in the literature that the sampling need not be uniform but should overweight initial time instants, but no rigorous explanation was provided for these choice. In this paper we take some prototypical examples and, under standard hypothesis concerning the neural network convergence, we show that the optimal time sampling follows a truncated exponential distribution. In particular we explain when the time sampling is best to be uniform and when it should not be. The findings are illustrated with numerical examples on linear equation, Burgers' equation and the Lorenz system.

Transformer for Times Series: an Application to the S&P500

The transformer models have been extensively used with good results in a wide area of machine learning applications including Large Language Models and image generation. Here, we inquire on the applicability of this approach to financial time series. We first describe the dataset construction for two prototypical situations: a mean reverting synthetic Ornstein-Uhlenbeck process on one hand and real S&P500 data on the other hand. Then, we present in detail the proposed Transformer architecture and finally we discuss some encouraging results. For the synthetic data we predict rather accurately the next move, and for the S&P500 we get some interesting results related to quadratic variation and volatility prediction.

On the Convergence Rate of the Stochastic Gradient Descent and application to a modified policy gradient for the Multi Armed Bandit

We present a self-contained proof of the convergence rate of the Stochastic Gradient Descent (SGD) when the learning rate follows an inverse time decays schedule; we next apply the results to the convergence of a modified form of policy gradient Multi-Armed Bandit (MAB) with $L2$ regularization.

Onflow: an online portfolio allocation algorithm

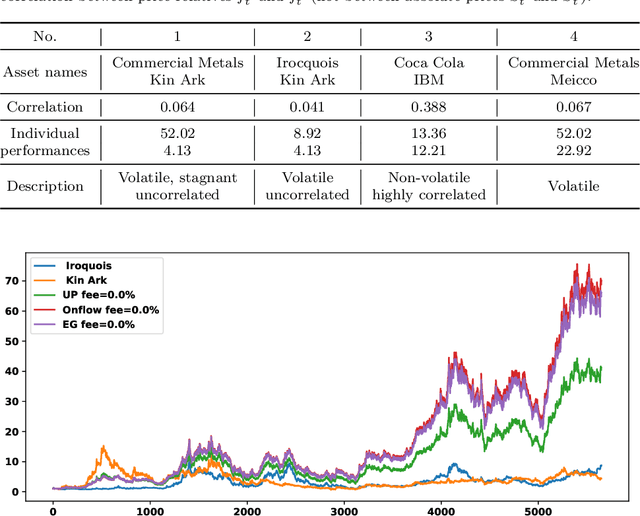
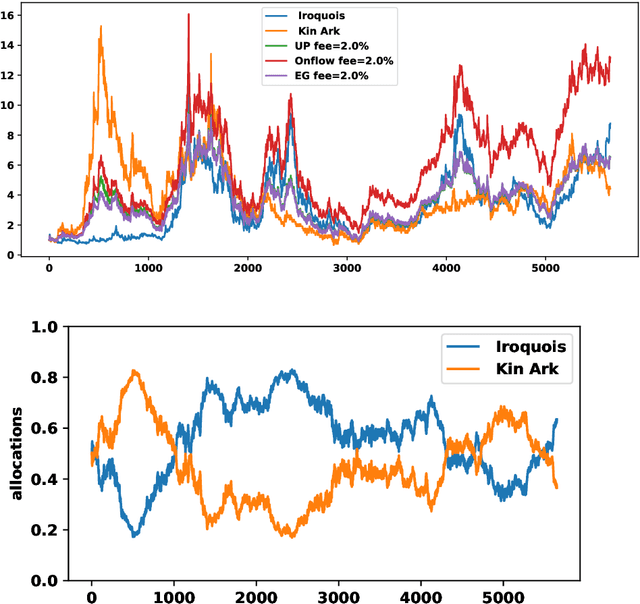
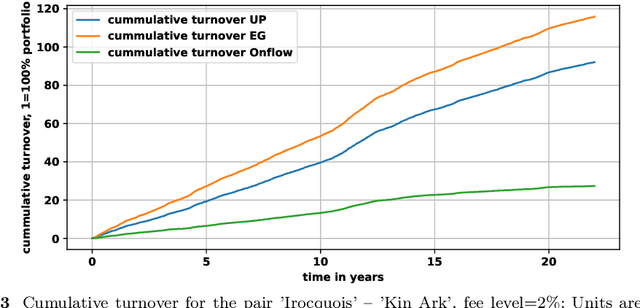
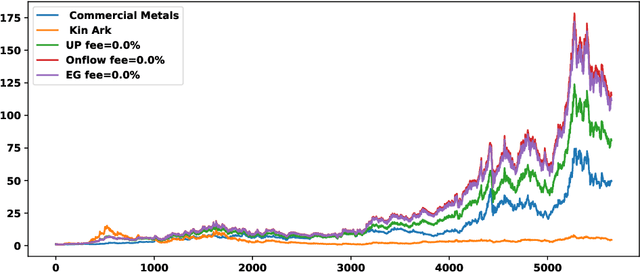
We introduce Onflow, a reinforcement learning technique that enables online optimization of portfolio allocation policies based on gradient flows. We devise dynamic allocations of an investment portfolio to maximize its expected log return while taking into account transaction fees. The portfolio allocation is parameterized through a softmax function, and at each time step, the gradient flow method leads to an ordinary differential equation whose solutions correspond to the updated allocations. This algorithm belongs to the large class of stochastic optimization procedures; we measure its efficiency by comparing our results to the mathematical theoretical values in a log-normal framework and to standard benchmarks from the 'old NYSE' dataset. For log-normal assets, the strategy learned by Onflow, with transaction costs at zero, mimics Markowitz's optimal portfolio and thus the best possible asset allocation strategy. Numerical experiments from the 'old NYSE' dataset show that Onflow leads to dynamic asset allocation strategies whose performances are: a) comparable to benchmark strategies such as Cover's Universal Portfolio or Helmbold et al. "multiplicative updates" approach when transaction costs are zero, and b) better than previous procedures when transaction costs are high. Onflow can even remain efficient in regimes where other dynamical allocation techniques do not work anymore. Therefore, as far as tested, Onflow appears to be a promising dynamic portfolio management strategy based on observed prices only and without any assumption on the laws of distributions of the underlying assets' returns. In particular it could avoid model risk when building a trading strategy.

Deep Conditional Measure Quantization

The quantization of a (probability) measure is replacing it by a sum of Dirac masses that is close enough to it (in some metric space of probability measures). Various methods exists to do so, but the situation of quantizing a conditional law has been less explored. We propose a method, called DCMQ, involving a Huber-energy kernel-based approach coupled with a deep neural network architecture. The method is tested on several examples and obtains promising results.

Huber-energy measure quantization

We describe a measure quantization procedure i.e., an algorithm which finds the best approximation of a target probability law (and more generally signed finite variation measure) by a sum of Q Dirac masses (Q being the quantization parameter). The procedure is implemented by minimizing the statistical distance between the original measure and its quantized version; the distance is built from a negative definite kernel and, if necessary, can be computed on the fly and feed to a stochastic optimization algorithm (such as SGD, Adam, ...). We investigate theoretically the fundamental questions of existence of the optimal measure quantizer and identify what are the required kernel properties that guarantee suitable behavior. We test the procedure, called HEMQ, on several databases: multi-dimensional Gaussian mixtures, Wiener space cubature, Italian wine cultivars and the MNIST image database. The results indicate that the HEMQ algorithm is robust and versatile and, for the class of Huber-energy kernels, it matches the expected intuitive behavior.

Diversity aware image generation

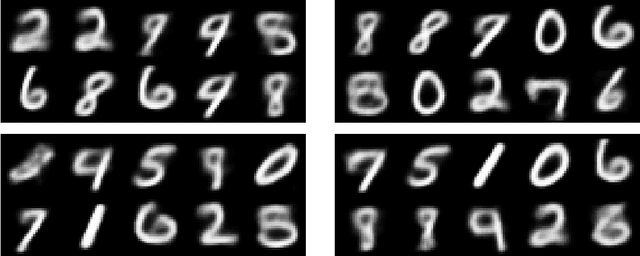
The machine learning generative algorithms such as GAN and VAE show impressive results in practice when constructing images similar to those in a training set. However, the generation of new images builds mainly on the understanding of the hidden structure of the training database followed by a mere sampling from a multi-dimensional normal variable. In particular each sample is independent from the other ones and can repeatedly propose same type of images. To cure this drawback we propose a kernel-based measure representation method that can produce new objects from a given target measure by approximating the measure as a whole and even staying away from objects already drawn from that distribution. This ensures a better variety of the produced images. The method is tested on some classic machine learning benchmarks.\end{abstract}

Algorithms that get old : the case of generative algorithms

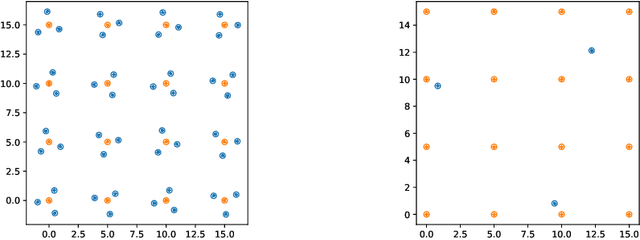
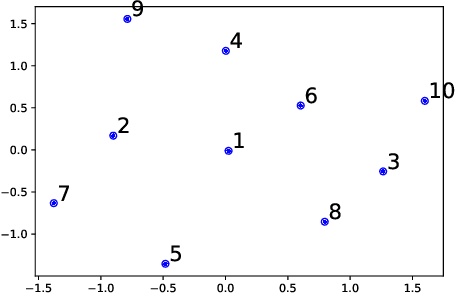
Generative IA networks, like the Variational Auto-Encoders (VAE), and Generative Adversarial Networks (GANs) produce new objects each time when asked to do so. However, this behavior is unlike that of human artists that change their style as times go by and seldom return to the initial point. We investigate a situation where VAEs are requested to sample from a probability measure described by some empirical set. Based on recent works on Radon-Sobolev statistical distances, we propose a numerical paradigm, to be used in conjunction with a generative algorithm, that satisfies the two following requirements: the objects created do not repeat and evolve to fill the entire target probability measure.

Convergence dynamics of Generative Adversarial Networks: the dual metric flows

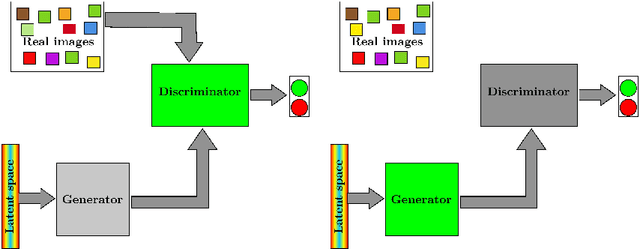
Fitting neural networks often resorts to stochastic (or similar) gradient descent which is a noise-tolerant (and efficient) resolution of a gradient descent dynamics. It outputs a sequence of networks parameters, which sequence evolves during the training steps. The gradient descent is the limit, when the learning rate is small and the batch size is infinite, of this set of increasingly optimal network parameters obtained during training. In this contribution, we investigate instead the convergence in the Generative Adversarial Networks used in machine learning. We study the limit of small learning rate, and show that, similar to single network training, the GAN learning dynamics tend, for vanishing learning rate to some limit dynamics. This leads us to consider evolution equations in metric spaces (which is the natural framework for evolving probability laws)that we call dual flows. We give formal definitions of solutions and prove the convergence. The theory is then applied to specific instances of GANs and we discuss how this insight helps understand and mitigate the mode collapse.