Convergence dynamics of Generative Adversarial Networks: the dual metric flows
Paper and Code
Dec 18, 2020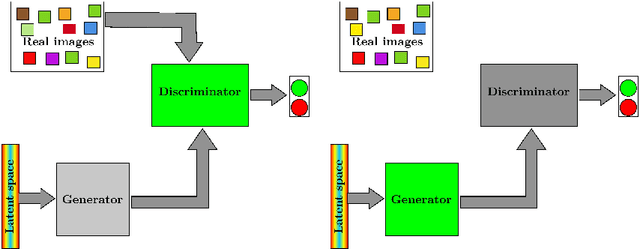
Fitting neural networks often resorts to stochastic (or similar) gradient descent which is a noise-tolerant (and efficient) resolution of a gradient descent dynamics. It outputs a sequence of networks parameters, which sequence evolves during the training steps. The gradient descent is the limit, when the learning rate is small and the batch size is infinite, of this set of increasingly optimal network parameters obtained during training. In this contribution, we investigate instead the convergence in the Generative Adversarial Networks used in machine learning. We study the limit of small learning rate, and show that, similar to single network training, the GAN learning dynamics tend, for vanishing learning rate to some limit dynamics. This leads us to consider evolution equations in metric spaces (which is the natural framework for evolving probability laws)that we call dual flows. We give formal definitions of solutions and prove the convergence. The theory is then applied to specific instances of GANs and we discuss how this insight helps understand and mitigate the mode collapse.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge