Learning Transient Convective Heat Transfer with Geometry Aware World Models

Partial differential equation (PDE) simulations are fundamental to engineering and physics but are often computationally prohibitive for real-time applications. While generative AI offers a promising avenue for surrogate modeling, standard video generation architectures lack the specific control and data compatibility required for physical simulations. This paper introduces a geometry aware world model architecture, derived from a video generation architecture (LongVideoGAN), designed to learn transient physics. We introduce two key architecture elements: (1) a twofold conditioning mechanism incorporating global physical parameters and local geometric masks, and (2) an architectural adaptation to support arbitrary channel dimensions, moving beyond standard RGB constraints. We evaluate this approach on a 2D transient computational fluid dynamics (CFD) problem involving convective heat transfer from buoyancy-driven flow coupled to a heat flow in a solid structure. We demonstrate that the conditioned model successfully reproduces complex temporal dynamics and spatial correlations of the training data. Furthermore, we assess the model's generalization capabilities on unseen geometric configurations, highlighting both its potential for controlled simulation synthesis and current limitations in spatial precision for out-of-distribution samples.

Generative Design of Ship Propellers using Conditional Flow Matching

In this paper, we explore the use of generative artificial intelligence (GenAI) for ship propeller design. While traditional forward machine learning models predict the performance of mechanical components based on given design parameters, GenAI models aim to generate designs that achieve specified performance targets. In particular, we employ conditional flow matching to establish a bidirectional mapping between design parameters and simulated noise that is conditioned on performance labels. This approach enables the generation of multiple valid designs corresponding to the same performance targets by sampling over the noise vector. To support model training, we generate data using a vortex lattice method for numerical simulation and analyze the trade-off between model accuracy and the amount of available data. We further propose data augmentation using pseudo-labels derived from less data-intensive forward surrogate models, which can often improve overall model performance. Finally, we present examples of distinct propeller geometries that exhibit nearly identical performance characteristics, illustrating the versatility and potential of GenAI in engineering design.

Consistency of Learned Sparse Grid Quadrature Rules using NeuralODEs

This paper provides a proof of the consistency of sparse grid quadrature for numerical integration of high dimensional distributions. In a first step, a transport map is learned that normalizes the distribution to a noise distribution on the unit cube. This step is built on the statistical learning theory of neural ordinary differential equations, which has been established recently. Secondly, the composition of the generative map with the quantity of interest is integrated numerically using the Clenshaw-Curtis sparse grid quadrature. A decomposition of the total numerical error in quadrature error and statistical error is provided. As main result it is proven in the framework of empirical risk minimization that all error terms can be controlled in the sense of PAC (probably approximately correct) learning and with high probability the numerical integral approximates the theoretical value up to an arbitrary small error in the limit where the data set size is growing and the network capacity is increased adaptively.

Towards Reliable Detection of Empty Space: Conditional Marked Point Processes for Object Detection

Deep neural networks have set the state-of-the-art in computer vision tasks such as bounding box detection and semantic segmentation. Object detectors and segmentation models assign confidence scores to predictions, reflecting the model's uncertainty in object detection or pixel-wise classification. However, these confidence estimates are often miscalibrated, as their architectures and loss functions are tailored to task performance rather than probabilistic foundation. Even with well calibrated predictions, object detectors fail to quantify uncertainty outside detected bounding boxes, i.e., the model does not make a probability assessment of whether an area without detected objects is truly free of obstacles. This poses a safety risk in applications such as automated driving, where uncertainty in empty areas remains unexplored. In this work, we propose an object detection model grounded in spatial statistics. Bounding box data matches realizations of a marked point process, commonly used to describe the probabilistic occurrence of spatial point events identified as bounding box centers, where marks are used to describe the spatial extension of bounding boxes and classes. Our statistical framework enables a likelihood-based training and provides well-defined confidence estimates for whether a region is drivable, i.e., free of objects. We demonstrate the effectiveness of our method through calibration assessments and evaluation of performance.

Robust Evolutionary Multi-Objective Network Architecture Search for Reinforcement Learning (EMNAS-RL)

This paper introduces Evolutionary Multi-Objective Network Architecture Search (EMNAS) for the first time to optimize neural network architectures in large-scale Reinforcement Learning (RL) for Autonomous Driving (AD). EMNAS uses genetic algorithms to automate network design, tailored to enhance rewards and reduce model size without compromising performance. Additionally, parallelization techniques are employed to accelerate the search, and teacher-student methodologies are implemented to ensure scalable optimization. This research underscores the potential of transfer learning as a robust framework for optimizing performance across iterative learning processes by effectively leveraging knowledge from earlier generations to enhance learning efficiency and stability in subsequent generations. Experimental results demonstrate that tailored EMNAS outperforms manually designed models, achieving higher rewards with fewer parameters. The findings of these strategies contribute positively to EMNAS for RL in autonomous driving, advancing the field toward better-performing networks suitable for real-world scenarios.

Generative AI for Autonomous Driving: A Review

Generative AI (GenAI) is rapidly advancing the field of Autonomous Driving (AD), extending beyond traditional applications in text, image, and video generation. We explore how generative models can enhance automotive tasks, such as static map creation, dynamic scenario generation, trajectory forecasting, and vehicle motion planning. By examining multiple generative approaches ranging from Variational Autoencoder (VAEs) over Generative Adversarial Networks (GANs) and Invertible Neural Networks (INNs) to Generative Transformers (GTs) and Diffusion Models (DMs), we highlight and compare their capabilities and limitations for AD-specific applications. Additionally, we discuss hybrid methods integrating conventional techniques with generative approaches, and emphasize their improved adaptability and robustness. We also identify relevant datasets and outline open research questions to guide future developments in GenAI. Finally, we discuss three core challenges: safety, interpretability, and realtime capabilities, and present recommendations for image generation, dynamic scenario generation, and planning.

Learning Brenier Potentials with Convex Generative Adversarial Neural Networks

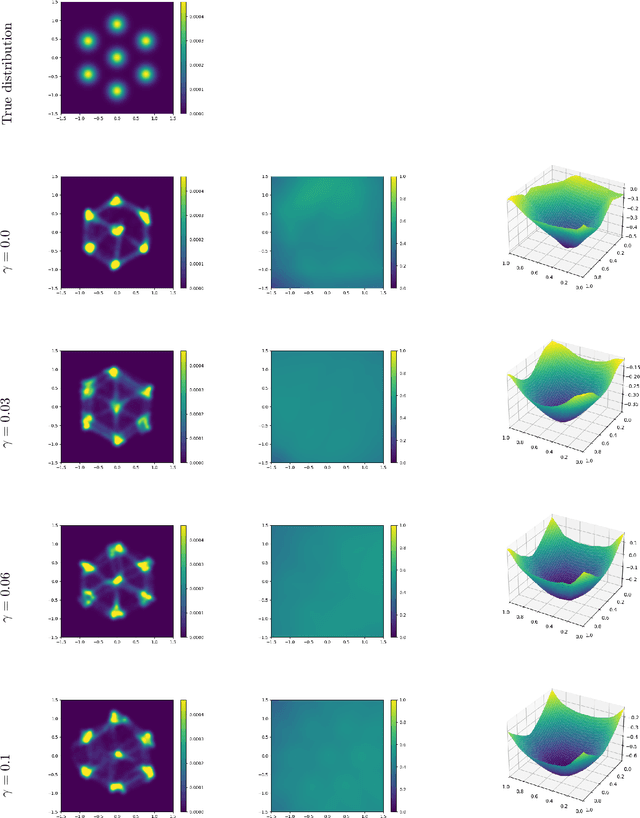
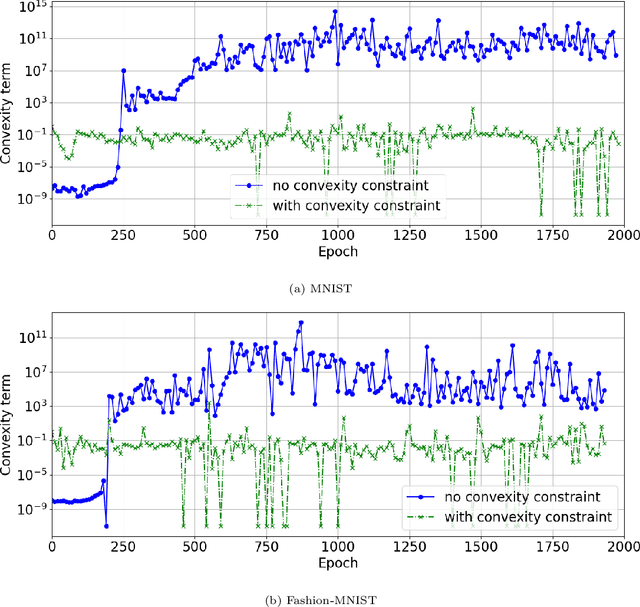
Brenier proved that under certain conditions on a source and a target probability measure there exists a strictly convex function such that its gradient is a transport map from the source to the target distribution. This function is called the Brenier potential. Furthermore, detailed information on the H\"older regularity of the Brenier potential is available. In this work we develop the statistical learning theory of generative adversarial neural networks that learn the Brenier potential. As by the transformation of densities formula, the density of the generated measure depends on the second derivative of the Brenier potential, we develop the universal approximation theory of ReCU networks with cubic activation $\mathtt{ReCU}(x)=\max\{0,x\}^3$ that combines the favorable approximation properties of H\"older functions with a Lipschitz continuous density. In order to assure the convexity of such general networks, we introduce an adversarial training procedure for a potential function represented by the ReCU networks that combines the classical discriminator cross entropy loss with a penalty term that enforces (strict) convexity. We give a detailed decomposition of learning errors and show that for a suitable high penalty parameter all networks chosen in the adversarial min-max optimization problem are strictly convex. This is further exploited to prove the consistency of the learning procedure for (slowly) expanding network capacity. We also implement the described learning algorithm and apply it to a number of standard test cases from Gaussian mixture to image data as target distributions. As predicted in theory, we observe that the convexity loss becomes inactive during the training process and the potentials represented by the neural networks have learned convexity.

Efficient Contrastive Decoding with Probabilistic Hallucination Detection - Mitigating Hallucinations in Large Vision Language Models -

Despite recent advances in Large Vision Language Models (LVLMs), these models still suffer from generating hallucinatory responses that do not align with the visual input provided. To mitigate such hallucinations, we introduce Efficient Contrastive Decoding (ECD), a simple method that leverages probabilistic hallucination detection to shift the output distribution towards contextually accurate answers at inference time. By contrasting token probabilities and hallucination scores, ECD subtracts hallucinated concepts from the original distribution, effectively suppressing hallucinations. Notably, our proposed method can be applied to any open-source LVLM and does not require additional LVLM training. We evaluate our method on several benchmark datasets and across different LVLMs. Our experiments show that ECD effectively mitigates hallucinations, outperforming state-of-the-art methods with respect to performance on LVLM benchmarks and computation time.

Numerical and statistical analysis of NeuralODE with Runge-Kutta time integration

NeuralODE is one example for generative machine learning based on the push forward of a simple source measure with a bijective mapping, which in the case of NeuralODE is given by the flow of a ordinary differential equation. Using Liouville's formula, the log-density of the push forward measure is easy to compute and thus NeuralODE can be trained based on the maximum Likelihood method such that the Kulback-Leibler divergence between the push forward through the flow map and the target measure generating the data becomes small. In this work, we give a detailed account on the consistency of Maximum Likelihood based empirical risk minimization for a generic class of target measures. In contrast to prior work, we do not only consider the statistical learning theory, but also give a detailed numerical analysis of the NeuralODE algorithm based on the 2nd order Runge-Kutta (RK) time integration. Using the universal approximation theory for deep ReQU networks, the stability and convergence rated for the RK scheme as well as metric entropy and concentration inequalities, we are able to prove that NeuralODE is a probably approximately correct (PAC) learning algorithm.

Segment-Level Road Obstacle Detection Using Visual Foundation Model Priors and Likelihood Ratios

Detecting road obstacles is essential for autonomous vehicles to navigate dynamic and complex traffic environments safely. Current road obstacle detection methods typically assign a score to each pixel and apply a threshold to generate final predictions. However, selecting an appropriate threshold is challenging, and the per-pixel classification approach often leads to fragmented predictions with numerous false positives. In this work, we propose a novel method that leverages segment-level features from visual foundation models and likelihood ratios to predict road obstacles directly. By focusing on segments rather than individual pixels, our approach enhances detection accuracy, reduces false positives, and offers increased robustness to scene variability. We benchmark our approach against existing methods on the RoadObstacle and LostAndFound datasets, achieving state-of-the-art performance without needing a predefined threshold.