Hyperparameter Optimization for Driving Strategies Based on Reinforcement Learning

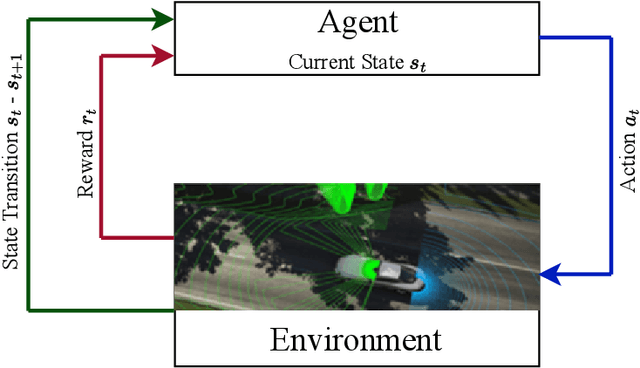
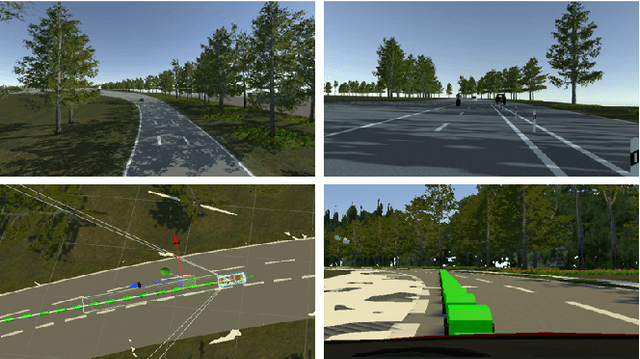
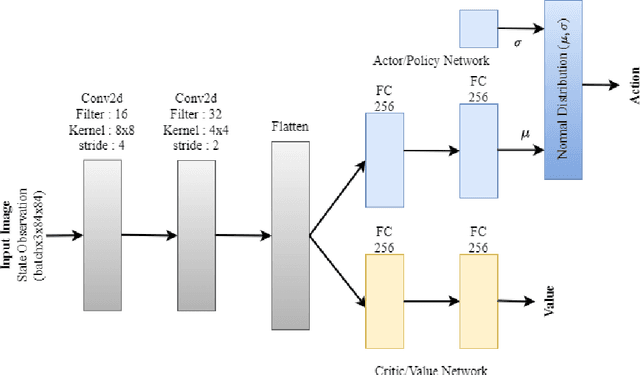
This paper focuses on hyperparameter optimization for autonomous driving strategies based on Reinforcement Learning. We provide a detailed description of training the RL agent in a simulation environment. Subsequently, we employ Efficient Global Optimization algorithm that uses Gaussian Process fitting for hyperparameter optimization in RL. Before this optimization phase, Gaussian process interpolation is applied to fit the surrogate model, for which the hyperparameter set is generated using Latin hypercube sampling. To accelerate the evaluation, parallelization techniques are employed. Following the hyperparameter optimization procedure, a set of hyperparameters is identified, resulting in a noteworthy enhancement in overall driving performance. There is a substantial increase of 4\% when compared to existing manually tuned parameters and the hyperparameters discovered during the initialization process using Latin hypercube sampling. After the optimization, we analyze the obtained results thoroughly and conduct a sensitivity analysis to assess the robustness and generalization capabilities of the learned autonomous driving strategies. The findings from this study contribute to the advancement of Gaussian process based Bayesian optimization to optimize the hyperparameters for autonomous driving in RL, providing valuable insights for the development of efficient and reliable autonomous driving systems.

Finding hidden-feature depending laws inside a data set and classifying it using Neural Network

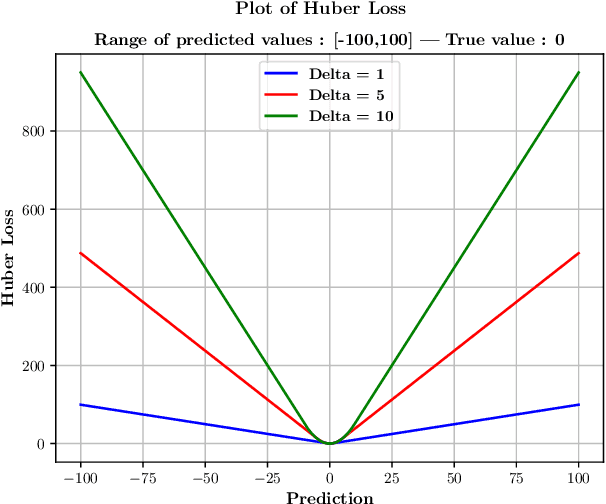
The logcosh loss function for neural networks has been developed to combine the advantage of the absolute error loss function of not overweighting outliers with the advantage of the mean square error of continuous derivative near the mean, which makes the last phase of learning easier. It is clear, and one experiences it soon, that in the case of clustered data, an artificial neural network with logcosh loss learns the bigger cluster rather than the mean of the two. Even more so, the ANN, when used for regression of a set-valued function, will learn a value close to one of the choices, in other words, one branch of the set-valued function, while a mean-square-error NN will learn the value in between. This work suggests a method that uses artificial neural networks with logcosh loss to find the branches of set-valued mappings in parameter-outcome sample sets and classifies the samples according to those branches.

Classification based on invisible features and thereby finding the effect of tuberculosis vaccine on COVID-19

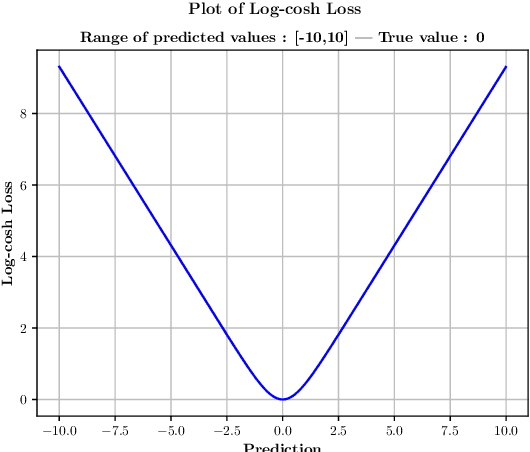
In the case of clustered data, an artificial neural network with logcosh loss function learns the bigger cluster rather than the mean of the two. Even more so, the ANN when used for regression of a set-valued function, will learn a value close to one of the choices, in other words, it learns one branch of the set-valued function with high accuracy. This work suggests a method that uses artificial neural networks with logcosh loss to find the branches of set-valued mappings in parameter-outcome sample sets and classifies the samples according to those branches. The method not only classifies the data based on these branches but also provides an accurate prediction for the majority cluster. The method successfully classifies the data based on an invisible feature. A neural network was successfully established to predict the total number of cases, the logarithmic total number of cases, deaths, active cases and other relevant data of the coronavirus for each German district from a number of input variables. As it has been speculated that the Tuberculosis vaccine provides protection against the virus and since East Germany was vaccinated before reunification, an attempt was made to classify the Eastern and Western German districts by considering the vaccine information as an invisible feature.