Fast Summation of Radial Kernels via QMC Slicing

The fast computation of large kernel sums is a challenging task, which arises as a subproblem in any kernel method. We approach the problem by slicing, which relies on random projections to one-dimensional subspaces and fast Fourier summation. We prove bounds for the slicing error and propose a quasi-Monte Carlo (QMC) approach for selecting the projections based on spherical quadrature rules. Numerical examples demonstrate that our QMC-slicing approach significantly outperforms existing methods like (QMC-)random Fourier features, orthogonal Fourier features or non-QMC slicing on standard test datasets.

Motion Detection in Diffraction Tomography by Common Circle Methods

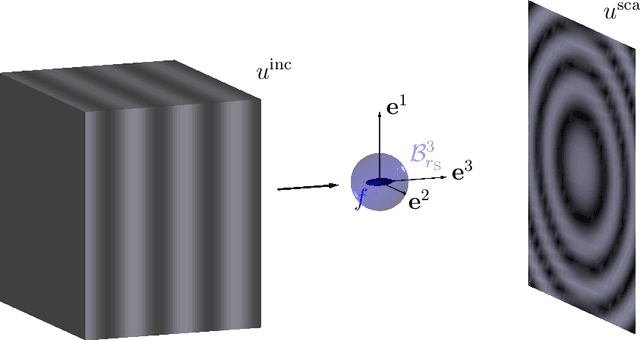
The method of common lines is a well-established reconstruction technique in cryogenic electron microscopy (cryo-EM), which can be used to extract the relative orientations of an object in tomographic projection images from different directions. In this paper, we deal with an analogous problem in optical diffraction tomography. Based on the Fourier diffraction theorem, we show that rigid motions, i.e., a map composed of rotations and translations, can be determined by detecting common circles in the Fourier-transformed data. We introduce two methods based on the idea of identifying common circles to reconstruct the object motion: While the first one is motivated by the common line approach for projection images and detects the relative orientation by the shape of the common circles in the two images, the second one assumes a smooth motion over time and calculates the angular velocity of the rotational motion from an infinitesimal version of the common circle method. Interestingly, using the stereographic projection, both methods can be reformulated as common line methods, but these lines are, in contrast to those used in cryo-EM, not confined to pass through the origin and allow for a full reconstruction of the relative orientation. Numerical proof-of-the-concept examples demonstrate the performance of our reconstruction methods.

Total variation-based phase retrieval for diffraction tomography

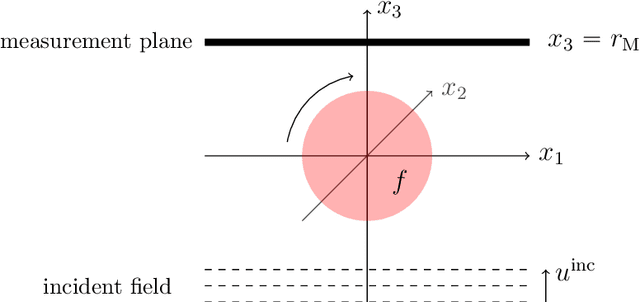
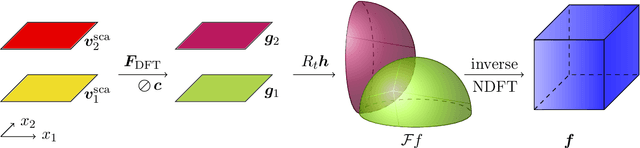
In optical diffraction tomography (ODT), the three-dimensional scattering potential of a microscopic object rotating around its center is recovered by a series of illuminations with coherent light. Reconstruction algorithms such as the filtered backpropagation require knowledge of the complex-valued wave at the measurement plane, whereas often only intensities, i.e., phaseless measurements, are available in practice. We propose a new reconstruction approach for ODT with unknown phase information based on three key ingredients. First, the light propagation is modeled using Born's approximation enabling us to use the Fourier diffraction theorem. Second, we stabilize the inversion of the non-uniform discrete Fourier transform via total variation regularization utilizing a primal-dual iteration, which also yields a novel numerical inversion formula for ODT with known phase. The third ingredient is a hybrid input-output scheme. We achieved convincing numerical results, which indicate that ODT with phaseless data is possible. The so-obtained 2D and 3D reconstructions are even comparable to the ones with known phase.