Taming Hyperparameter Tuning in Continuous Normalizing Flows Using the JKO Scheme

A normalizing flow (NF) is a mapping that transforms a chosen probability distribution to a normal distribution. Such flows are a common technique used for data generation and density estimation in machine learning and data science. The density estimate obtained with a NF requires a change of variables formula that involves the computation of the Jacobian determinant of the NF transformation. In order to tractably compute this determinant, continuous normalizing flows (CNF) estimate the mapping and its Jacobian determinant using a neural ODE. Optimal transport (OT) theory has been successfully used to assist in finding CNFs by formulating them as OT problems with a soft penalty for enforcing the standard normal distribution as a target measure. A drawback of OT-based CNFs is the addition of a hyperparameter, $\alpha$, that controls the strength of the soft penalty and requires significant tuning. We present JKO-Flow, an algorithm to solve OT-based CNF without the need of tuning $\alpha$. This is achieved by integrating the OT CNF framework into a Wasserstein gradient flow framework, also known as the JKO scheme. Instead of tuning $\alpha$, we repeatedly solve the optimization problem for a fixed $\alpha$ effectively performing a JKO update with a time-step $\alpha$. Hence we obtain a "divide and conquer" algorithm by repeatedly solving simpler problems instead of solving a potentially harder problem with large $\alpha$.

Estimating a potential without the agony of the partition function

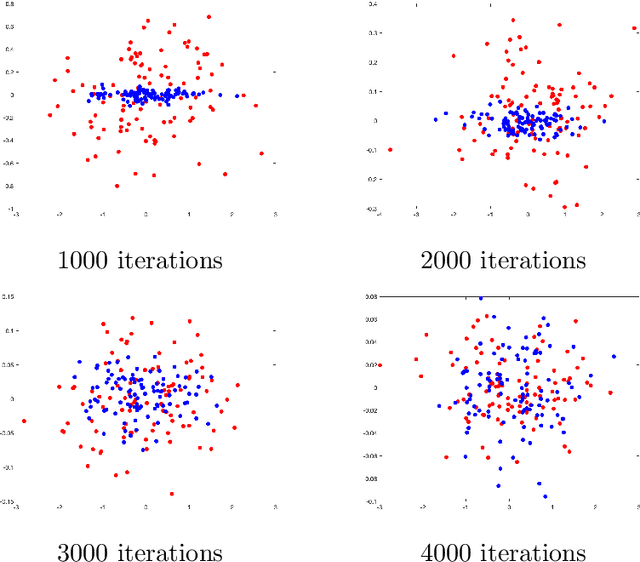
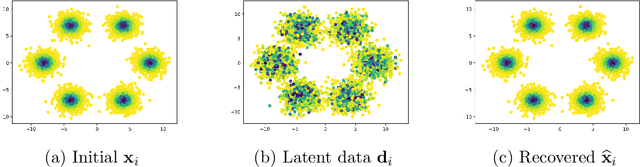
Estimating a Gibbs density function given a sample is an important problem in computational statistics and statistical learning. Although the well established maximum likelihood method is commonly used, it requires the computation of the partition function (i.e., the normalization of the density). This function can be easily calculated for simple low-dimensional problems but its computation is difficult or even intractable for general densities and high-dimensional problems. In this paper we propose an alternative approach based on Maximum A-Posteriori (MAP) estimators, we name Maximum Recovery MAP (MR-MAP), to derive estimators that do not require the computation of the partition function, and reformulate the problem as an optimization problem. We further propose a least-action type potential that allows us to quickly solve the optimization problem as a feed-forward hyperbolic neural network. We demonstrate the effectiveness of our methods on some standard data sets.

Stochastic Newton and Quasi-Newton Methods for Large Linear Least-squares Problems

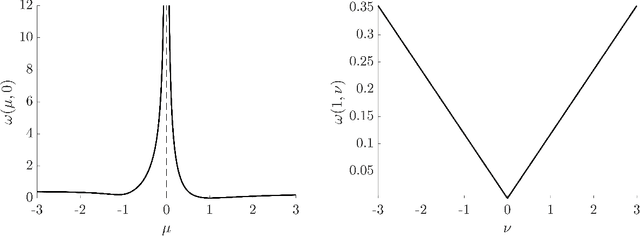
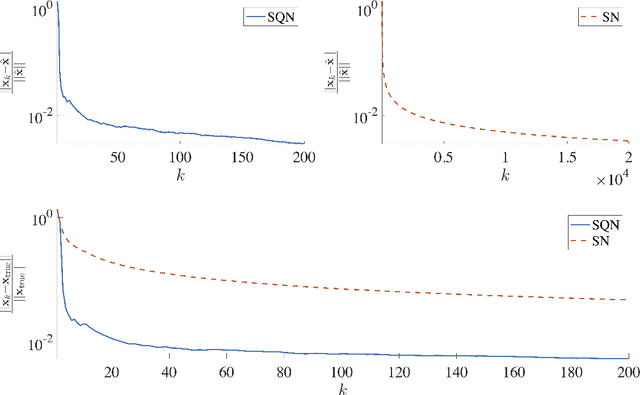
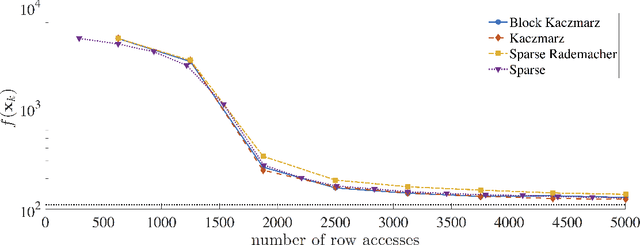
We describe stochastic Newton and stochastic quasi-Newton approaches to efficiently solve large linear least-squares problems where the very large data sets present a significant computational burden (e.g., the size may exceed computer memory or data are collected in real-time). In our proposed framework, stochasticity is introduced in two different frameworks as a means to overcome these computational limitations, and probability distributions that can exploit structure and/or sparsity are considered. Theoretical results on consistency of the approximations for both the stochastic Newton and the stochastic quasi-Newton methods are provided. The results show, in particular, that stochastic Newton iterates, in contrast to stochastic quasi-Newton iterates, may not converge to the desired least-squares solution. Numerical examples, including an example from extreme learning machines, demonstrate the potential applications of these methods.