Samy Wu Fung
Colorado School of Mines, Department of Applied Mathematics and Statistics
On the Convergence of Jacobian-Free Backpropagation for Optimal Control Problems with Implicit Hamiltonians
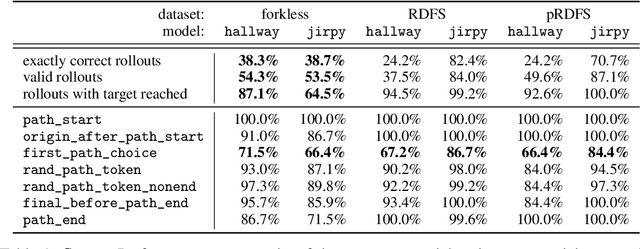
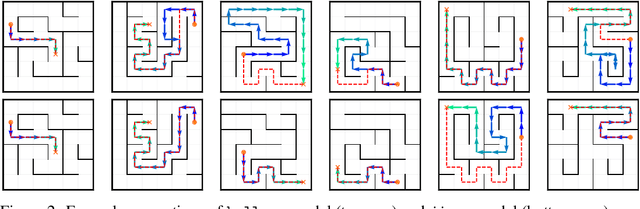
Jan 31, 2026Abstract:Optimal feedback control with implicit Hamiltonians poses a fundamental challenge for learning-based value function methods due to the absence of closed-form optimal control laws. Recent work~\cite{gelphman2025end} introduced an implicit deep learning approach using Jacobian-Free Backpropagation (JFB) to address this setting, but only established sample-wise descent guarantees. In this paper, we establish convergence guarantees for JFB in the stochastic minibatch setting, showing that the resulting updates converge to stationary points of the expected optimal control objective. We further demonstrate scalability on substantially higher-dimensional problems, including multi-agent optimal consumption and swarm-based quadrotor and bicycle control. Together, our results provide both theoretical justification and empirical evidence for using JFB in high-dimensional optimal control with implicit Hamiltonians.
A Generalization Bound for a Family of Implicit Networks
Oct 09, 2024

Abstract:Implicit networks are a class of neural networks whose outputs are defined by the fixed point of a parameterized operator. They have enjoyed success in many applications including natural language processing, image processing, and numerous other applications. While they have found abundant empirical success, theoretical work on its generalization is still under-explored. In this work, we consider a large family of implicit networks defined parameterized contractive fixed point operators. We show a generalization bound for this class based on a covering number argument for the Rademacher complexity of these architectures.
On Logical Extrapolation for Mazes with Recurrent and Implicit Networks
Oct 03, 2024



Abstract:Recent work has suggested that certain neural network architectures-particularly recurrent neural networks (RNNs) and implicit neural networks (INNs) are capable of logical extrapolation. That is, one may train such a network on easy instances of a specific task and then apply it successfully to more difficult instances of the same task. In this paper, we revisit this idea and show that (i) The capacity for extrapolation is less robust than previously suggested. Specifically, in the context of a maze-solving task, we show that while INNs (and some RNNs) are capable of generalizing to larger maze instances, they fail to generalize along axes of difficulty other than maze size. (ii) Models that are explicitly trained to converge to a fixed point (e.g. the INN we test) are likely to do so when extrapolating, while models that are not (e.g. the RNN we test) may exhibit more exotic limiting behaviour such as limit cycles, even when they correctly solve the problem. Our results suggest that (i) further study into why such networks extrapolate easily along certain axes of difficulty yet struggle with others is necessary, and (ii) analyzing the dynamics of extrapolation may yield insights into designing more efficient and interpretable logical extrapolators.
Structured World Representations in Maze-Solving Transformers
Dec 05, 2023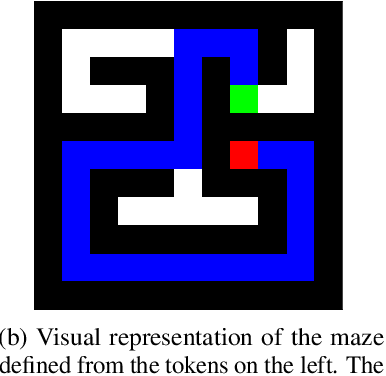

Abstract:Transformer models underpin many recent advances in practical machine learning applications, yet understanding their internal behavior continues to elude researchers. Given the size and complexity of these models, forming a comprehensive picture of their inner workings remains a significant challenge. To this end, we set out to understand small transformer models in a more tractable setting: that of solving mazes. In this work, we focus on the abstractions formed by these models and find evidence for the consistent emergence of structured internal representations of maze topology and valid paths. We demonstrate this by showing that the residual stream of only a single token can be linearly decoded to faithfully reconstruct the entire maze. We also find that the learned embeddings of individual tokens have spatial structure. Furthermore, we take steps towards deciphering the circuity of path-following by identifying attention heads (dubbed $\textit{adjacency heads}$), which are implicated in finding valid subsequent tokens.
A Configurable Library for Generating and Manipulating Maze Datasets
Sep 19, 2023



Abstract:Understanding how machine learning models respond to distributional shifts is a key research challenge. Mazes serve as an excellent testbed due to varied generation algorithms offering a nuanced platform to simulate both subtle and pronounced distributional shifts. To enable systematic investigations of model behavior on out-of-distribution data, we present $\texttt{maze-dataset}$, a comprehensive library for generating, processing, and visualizing datasets consisting of maze-solving tasks. With this library, researchers can easily create datasets, having extensive control over the generation algorithm used, the parameters fed to the algorithm of choice, and the filters that generated mazes must satisfy. Furthermore, it supports multiple output formats, including rasterized and text-based, catering to convolutional neural networks and autoregressive transformer models. These formats, along with tools for visualizing and converting between them, ensure versatility and adaptability in research applications.
Faster Predict-and-Optimize with Three-Operator Splitting
Jan 31, 2023Abstract:In many practical settings, a combinatorial problem must be repeatedly solved with similar, but distinct parameters w. Yet, w is not directly observed; only contextual data d that correlates with w is available. It is tempting to use a neural network to predict w given d, but training such a model requires reconciling the discrete nature of combinatorial optimization with the gradient-based frameworks used to train neural networks. One approach to overcoming this issue is to consider a continuous relaxation of the combinatorial problem. While existing such approaches have shown to be highly effective on small problems (10-100 variables) they do not scale well to large problems. In this work, we show how recent results in operator splitting can be used to design such a system which is easy to train and scales effortlessly to problems with thousands of variables.
Taming Hyperparameter Tuning in Continuous Normalizing Flows Using the JKO Scheme
Nov 30, 2022Abstract:A normalizing flow (NF) is a mapping that transforms a chosen probability distribution to a normal distribution. Such flows are a common technique used for data generation and density estimation in machine learning and data science. The density estimate obtained with a NF requires a change of variables formula that involves the computation of the Jacobian determinant of the NF transformation. In order to tractably compute this determinant, continuous normalizing flows (CNF) estimate the mapping and its Jacobian determinant using a neural ODE. Optimal transport (OT) theory has been successfully used to assist in finding CNFs by formulating them as OT problems with a soft penalty for enforcing the standard normal distribution as a target measure. A drawback of OT-based CNFs is the addition of a hyperparameter, $\alpha$, that controls the strength of the soft penalty and requires significant tuning. We present JKO-Flow, an algorithm to solve OT-based CNF without the need of tuning $\alpha$. This is achieved by integrating the OT CNF framework into a Wasserstein gradient flow framework, also known as the JKO scheme. Instead of tuning $\alpha$, we repeatedly solve the optimization problem for a fixed $\alpha$ effectively performing a JKO update with a time-step $\alpha$. Hence we obtain a "divide and conquer" algorithm by repeatedly solving simpler problems instead of solving a potentially harder problem with large $\alpha$.
Explainable AI via Learning to Optimize
Apr 29, 2022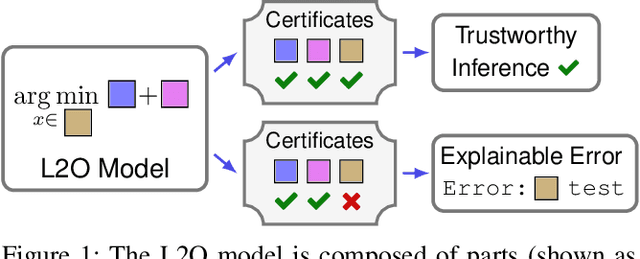
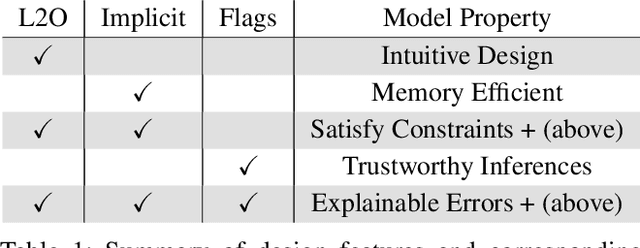
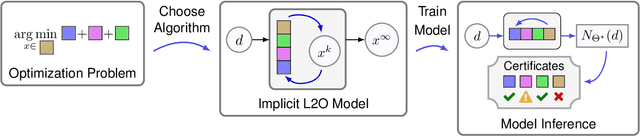
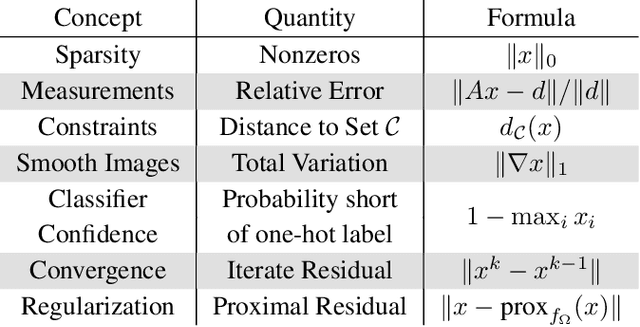
Abstract:Indecipherable black boxes are common in machine learning (ML), but applications increasingly require explainable artificial intelligence (XAI). The core of XAI is to establish transparent and interpretable data-driven algorithms. This work provides concrete tools for XAI in situations where prior knowledge must be encoded and untrustworthy inferences flagged. We use the "learn to optimize" (L2O) methodology wherein each inference solves a data-driven optimization problem. Our L2O models are straightforward to implement, directly encode prior knowledge, and yield theoretical guarantees (e.g. satisfaction of constraints). We also propose use of interpretable certificates to verify whether model inferences are trustworthy. Numerical examples are provided in the applications of dictionary-based signal recovery, CT imaging, and arbitrage trading of cryptoassets.
Learn to Predict Equilibria via Fixed Point Networks
Jun 02, 2021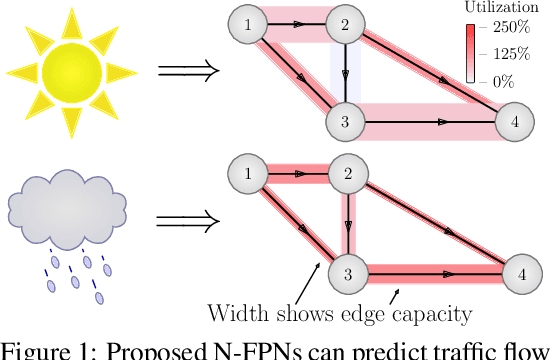

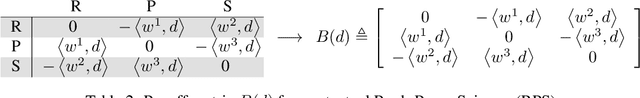
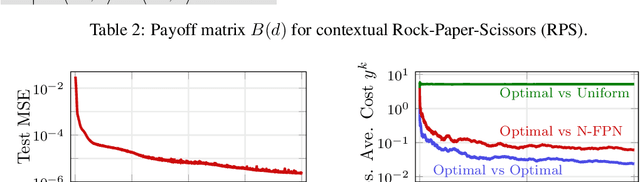
Abstract:Systems of interacting agents can often be modeled as contextual games, where the context encodes additional information, beyond the control of any agent (e.g. weather for traffic and fiscal policy for market economies). In such systems, the most likely outcome is given by a Nash equilibrium. In many practical settings, only game equilibria are observed, while the optimal parameters for a game model are unknown. This work introduces Nash Fixed Point Networks (N-FPNs), a class of implicit-depth neural networks that output Nash equilibria of contextual games. The N-FPN architecture fuses data-driven modeling with provided constraints. Given equilibrium observations of a contextual game, N-FPN parameters are learnt to predict equilibria outcomes given only the context. We present an end-to-end training scheme for N-FPNs that is simple and memory efficient to implement with existing autodifferentiation tools. N-FPNs also exploit a novel constraint decoupling scheme to avoid costly projections. Provided numerical examples show the efficacy of N-FPNs on atomic and non-atomic games (e.g. traffic routing).
Feasibility-based Fixed Point Networks
Apr 29, 2021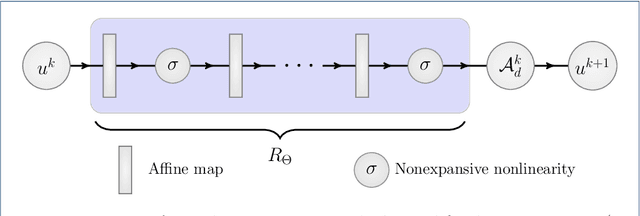
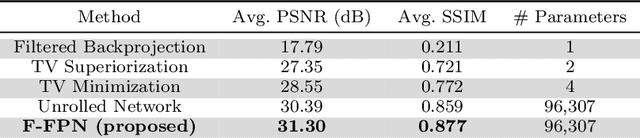

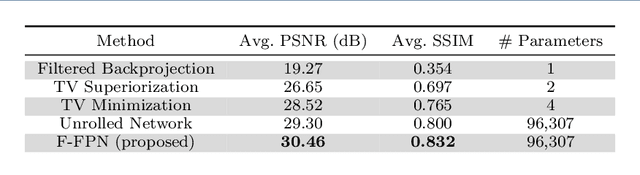
Abstract:Inverse problems consist of recovering a signal from a collection of noisy measurements. These problems can often be cast as feasibility problems; however, additional regularization is typically necessary to ensure accurate and stable recovery with respect to data perturbations. Hand-chosen analytic regularization can yield desirable theoretical guarantees, but such approaches have limited effectiveness recovering signals due to their inability to leverage large amounts of available data. To this end, this work fuses data-driven regularization and convex feasibility in a theoretically sound manner. This is accomplished using feasibility-based fixed point networks (F-FPNs). Each F-FPN defines a collection of nonexpansive operators, each of which is the composition of a projection-based operator and a data-driven regularization operator. Fixed point iteration is used to compute fixed points of these operators, and weights of the operators are tuned so that the fixed points closely represent available data. Numerical examples demonstrate performance increases by F-FPNs when compared to standard TV-based recovery methods for CT reconstruction and a comparable neural network based on algorithm unrolling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge