Fixed Point Networks: Implicit Depth Models with Jacobian-Free Backprop

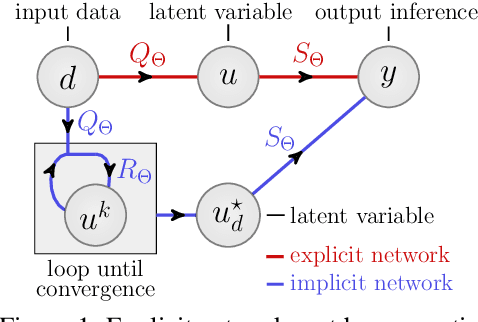
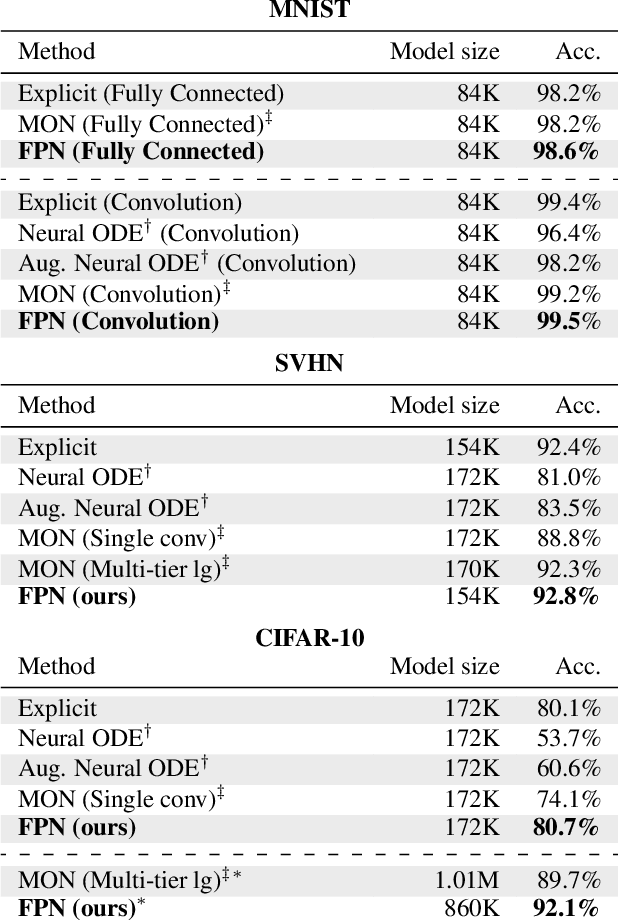
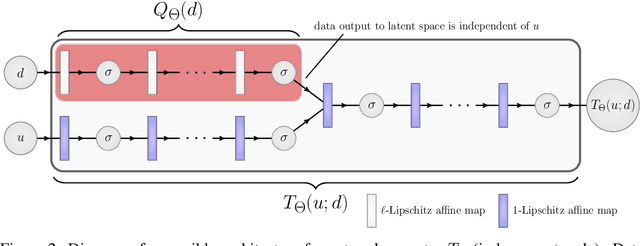
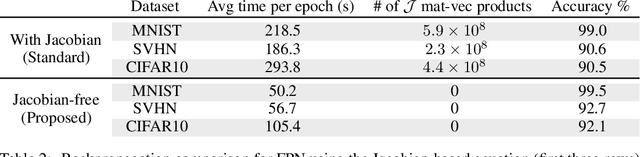
A growing trend in deep learning replaces fixed depth models by approximations of the limit as network depth approaches infinity. This approach uses a portion of network weights to prescribe behavior by defining a limit condition. This makes network depth implicit, varying based on the provided data and an error tolerance. Moreover, existing implicit models can be implemented and trained with fixed memory costs in exchange for additional computational costs. In particular, backpropagation through implicit depth models requires solving a Jacobian-based equation arising from the implicit function theorem. We propose fixed point networks (FPNs), a simple setup for implicit depth learning that guarantees convergence of forward propagation to a unique limit defined by network weights and input data. Our key contribution is to provide a new Jacobian-free backpropagation (JFB) scheme that circumvents the need to solve Jacobian-based equations while maintaining fixed memory costs. This makes FPNs much cheaper to train and easy to implement. Our numerical examples yield state of the art classification results for implicit depth models and outperform corresponding explicit models.