Faster Predict-and-Optimize with Three-Operator Splitting

In many practical settings, a combinatorial problem must be repeatedly solved with similar, but distinct parameters w. Yet, w is not directly observed; only contextual data d that correlates with w is available. It is tempting to use a neural network to predict w given d, but training such a model requires reconciling the discrete nature of combinatorial optimization with the gradient-based frameworks used to train neural networks. One approach to overcoming this issue is to consider a continuous relaxation of the combinatorial problem. While existing such approaches have shown to be highly effective on small problems (10-100 variables) they do not scale well to large problems. In this work, we show how recent results in operator splitting can be used to design such a system which is easy to train and scales effortlessly to problems with thousands of variables.

Explainable AI via Learning to Optimize

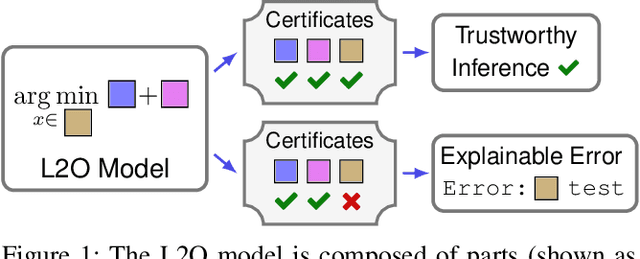
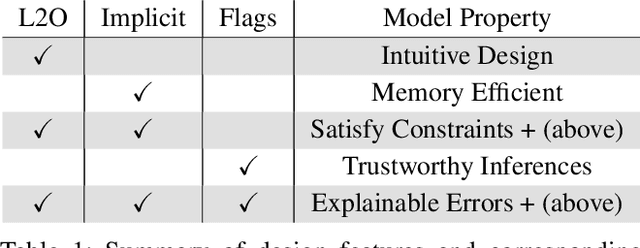
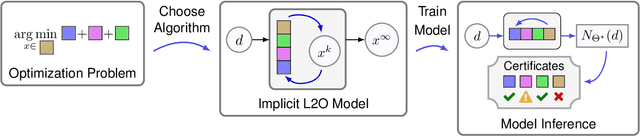
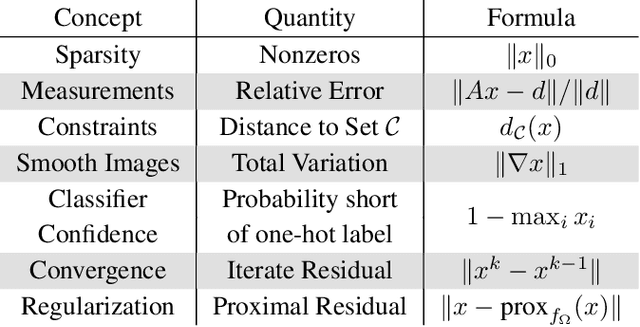
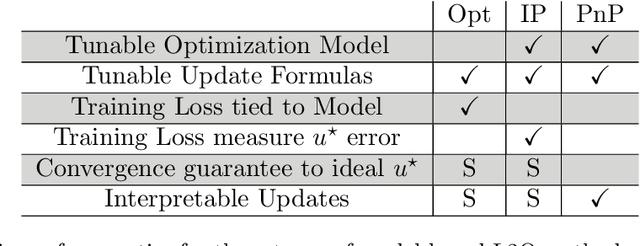
Indecipherable black boxes are common in machine learning (ML), but applications increasingly require explainable artificial intelligence (XAI). The core of XAI is to establish transparent and interpretable data-driven algorithms. This work provides concrete tools for XAI in situations where prior knowledge must be encoded and untrustworthy inferences flagged. We use the "learn to optimize" (L2O) methodology wherein each inference solves a data-driven optimization problem. Our L2O models are straightforward to implement, directly encode prior knowledge, and yield theoretical guarantees (e.g. satisfaction of constraints). We also propose use of interpretable certificates to verify whether model inferences are trustworthy. Numerical examples are provided in the applications of dictionary-based signal recovery, CT imaging, and arbitrage trading of cryptoassets.

Learn to Predict Equilibria via Fixed Point Networks

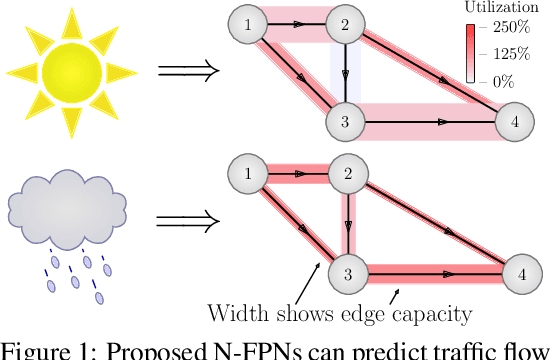
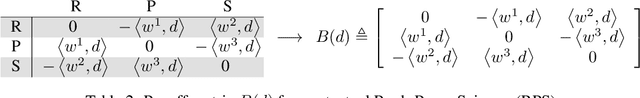
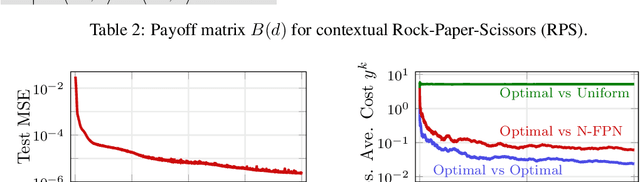
Systems of interacting agents can often be modeled as contextual games, where the context encodes additional information, beyond the control of any agent (e.g. weather for traffic and fiscal policy for market economies). In such systems, the most likely outcome is given by a Nash equilibrium. In many practical settings, only game equilibria are observed, while the optimal parameters for a game model are unknown. This work introduces Nash Fixed Point Networks (N-FPNs), a class of implicit-depth neural networks that output Nash equilibria of contextual games. The N-FPN architecture fuses data-driven modeling with provided constraints. Given equilibrium observations of a contextual game, N-FPN parameters are learnt to predict equilibria outcomes given only the context. We present an end-to-end training scheme for N-FPNs that is simple and memory efficient to implement with existing autodifferentiation tools. N-FPNs also exploit a novel constraint decoupling scheme to avoid costly projections. Provided numerical examples show the efficacy of N-FPNs on atomic and non-atomic games (e.g. traffic routing).

Feasibility-based Fixed Point Networks

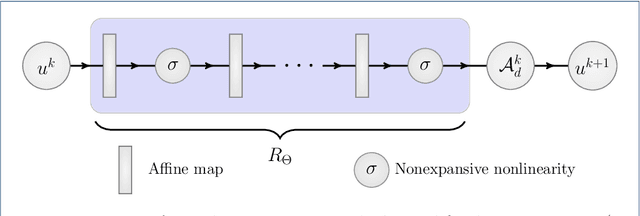
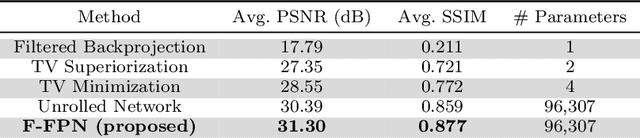
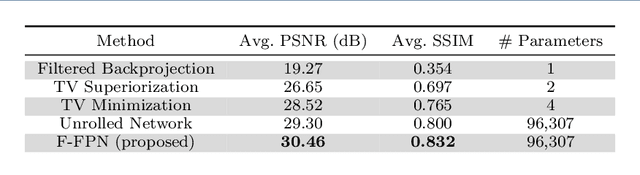
Inverse problems consist of recovering a signal from a collection of noisy measurements. These problems can often be cast as feasibility problems; however, additional regularization is typically necessary to ensure accurate and stable recovery with respect to data perturbations. Hand-chosen analytic regularization can yield desirable theoretical guarantees, but such approaches have limited effectiveness recovering signals due to their inability to leverage large amounts of available data. To this end, this work fuses data-driven regularization and convex feasibility in a theoretically sound manner. This is accomplished using feasibility-based fixed point networks (F-FPNs). Each F-FPN defines a collection of nonexpansive operators, each of which is the composition of a projection-based operator and a data-driven regularization operator. Fixed point iteration is used to compute fixed points of these operators, and weights of the operators are tuned so that the fixed points closely represent available data. Numerical examples demonstrate performance increases by F-FPNs when compared to standard TV-based recovery methods for CT reconstruction and a comparable neural network based on algorithm unrolling.

Learning to Optimize: A Primer and A Benchmark

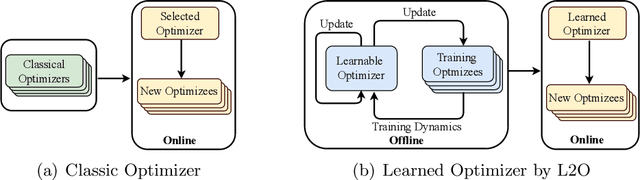
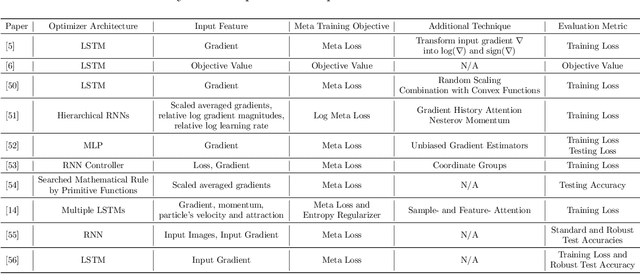
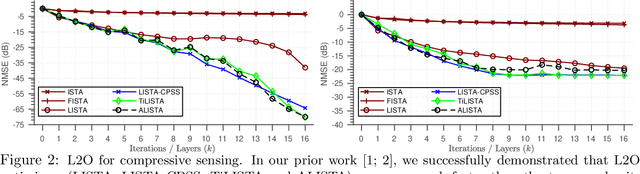
Learning to optimize (L2O) is an emerging approach that leverages machine learning to develop optimization methods, aiming at reducing the laborious iterations of hand engineering. It automates the design of an optimization method based on its performance on a set of training problems. This data-driven procedure generates methods that can efficiently solve problems similar to those in the training. In sharp contrast, the typical and traditional designs of optimization methods are theory-driven, so they obtain performance guarantees over the classes of problems specified by the theory. The difference makes L2O suitable for repeatedly solving a certain type of optimization problems over a specific distribution of data, while it typically fails on out-of-distribution problems. The practicality of L2O depends on the type of target optimization, the chosen architecture of the method to learn, and the training procedure. This new paradigm has motivated a community of researchers to explore L2O and report their findings. This article is poised to be the first comprehensive survey and benchmark of L2O for continuous optimization. We set up taxonomies, categorize existing works and research directions, present insights, and identify open challenges. We also benchmarked many existing L2O approaches on a few but representative optimization problems. For reproducible research and fair benchmarking purposes, we released our software implementation and data in the package Open-L2O at https://github.com/VITA-Group/Open-L2O.

Fixed Point Networks: Implicit Depth Models with Jacobian-Free Backprop

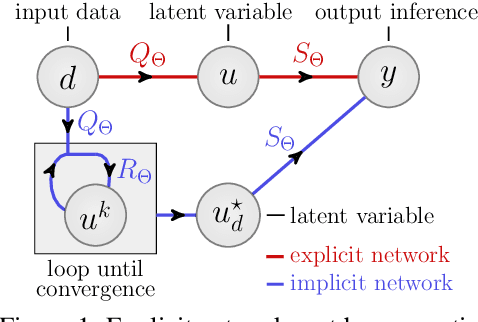
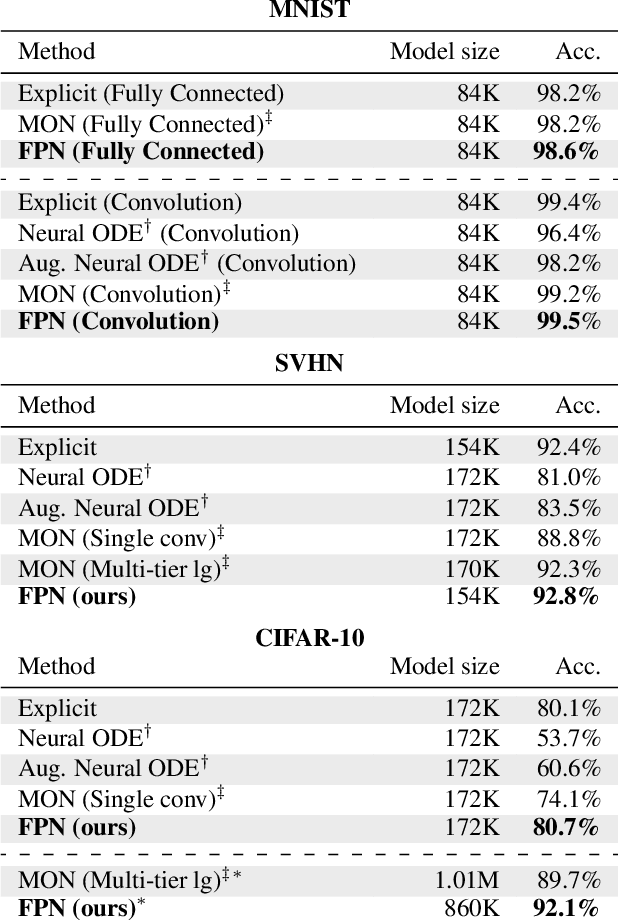
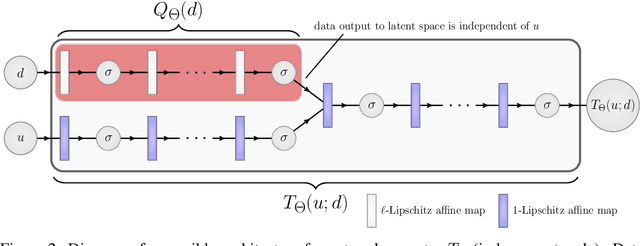
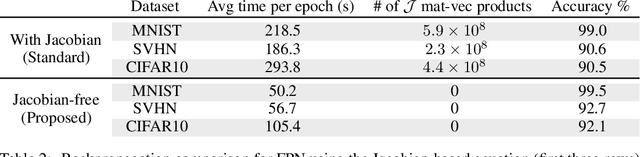
A growing trend in deep learning replaces fixed depth models by approximations of the limit as network depth approaches infinity. This approach uses a portion of network weights to prescribe behavior by defining a limit condition. This makes network depth implicit, varying based on the provided data and an error tolerance. Moreover, existing implicit models can be implemented and trained with fixed memory costs in exchange for additional computational costs. In particular, backpropagation through implicit depth models requires solving a Jacobian-based equation arising from the implicit function theorem. We propose fixed point networks (FPNs), a simple setup for implicit depth learning that guarantees convergence of forward propagation to a unique limit defined by network weights and input data. Our key contribution is to provide a new Jacobian-free backpropagation (JFB) scheme that circumvents the need to solve Jacobian-based equations while maintaining fixed memory costs. This makes FPNs much cheaper to train and easy to implement. Our numerical examples yield state of the art classification results for implicit depth models and outperform corresponding explicit models.

Projecting to Manifolds via Unsupervised Learning

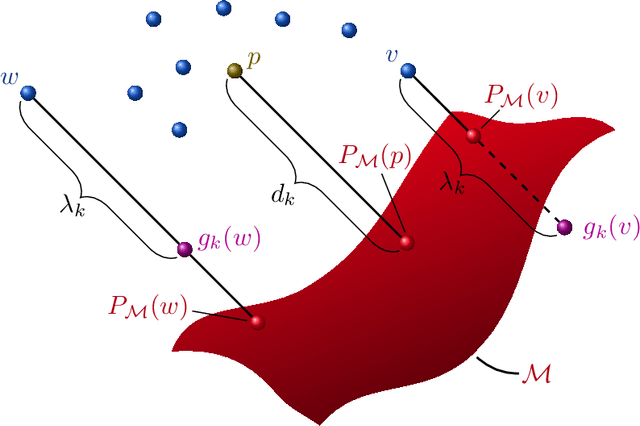
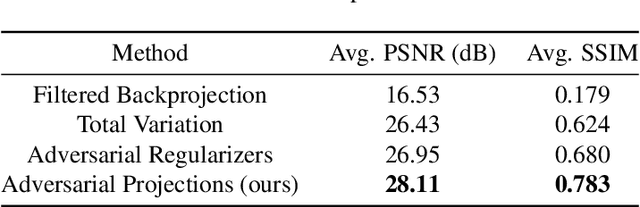
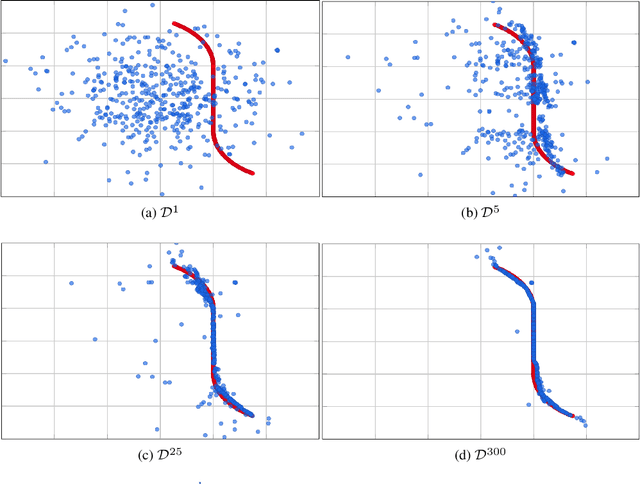
We present a new framework, called adversarial projections, for solving inverse problems by learning to project onto manifolds. Our goal is to recover a signal from a collection of noisy measurements. Traditional methods for this task often minimize the addition of a regularization term and an expression that measures compliance with measurements (e.g., least squares). However, it has been shown that convex regularization can introduce bias, preventing recovery of the true signal. Our approach avoids this issue by iteratively projecting signals toward the (possibly nonlinear) manifold of true signals. This is accomplished by first solving a sequence of unsupervised learning problems. The solution to each learning problem provides a collection of parameters that enables access to an iteration-dependent step size and access to the direction to project each signal toward the closest true signal. Given a signal estimate (e.g., recovered from a pseudo-inverse), we prove our method generates a sequence that converges in mean square to the projection onto this manifold. Several numerical illustrations are provided.

Safeguarded Learned Convex Optimization

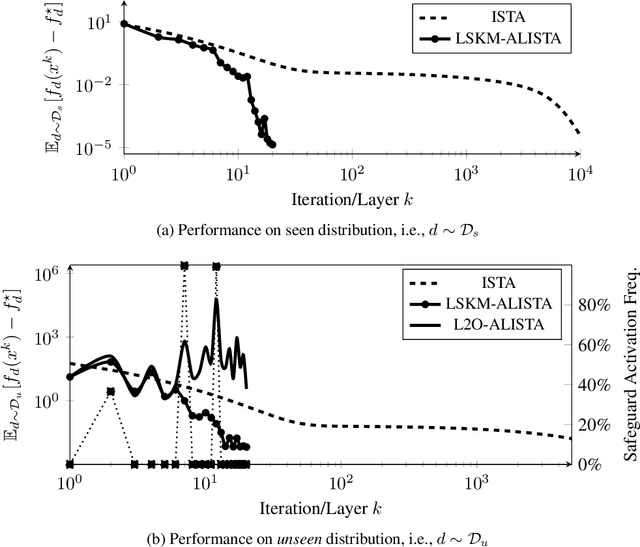
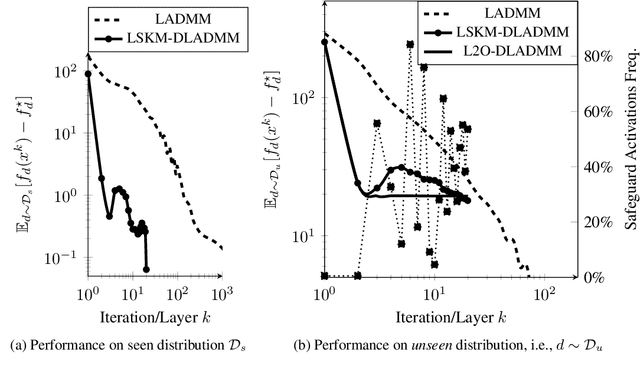
Many applications require repeatedly solving a certain type of optimization problem, each time with new (but similar) data. Data-driven algorithms can "learn to optimize" (L2O) with much fewer iterations and with similar cost per iteration as general-purpose optimization algorithms. L2O algorithms are often derived from general-purpose algorithms, but with the inclusion of (possibly many) tunable parameters. Exceptional performance has been demonstrated when the parameters are optimized for a particular distribution of data. Unfortunately, it is impossible to ensure all L2O algorithms always converge to a solution. However, we present a framework that uses L2O updates together with a safeguard to guarantee convergence for convex problems with proximal and/or gradient oracles. The safeguard is simple and computationally cheap to implement, and it should be activated only when the current L2O updates would perform poorly or appear to diverge. This approach yields the numerical benefits of employing machine learning methods to create rapid L2O algorithms while still guaranteeing convergence. Our numerical examples demonstrate the efficacy of this approach for existing and new L2O schemes.