Projecting to Manifolds via Unsupervised Learning

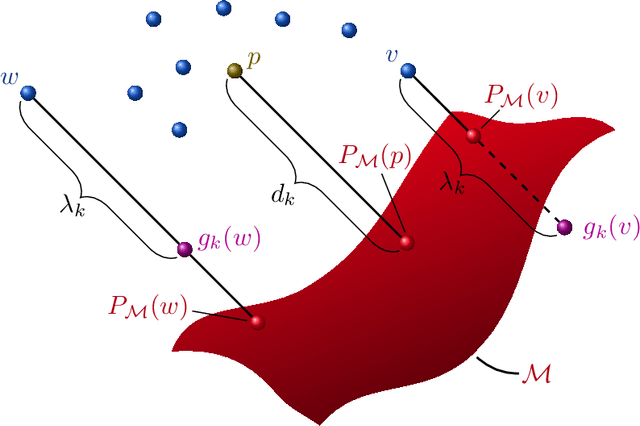
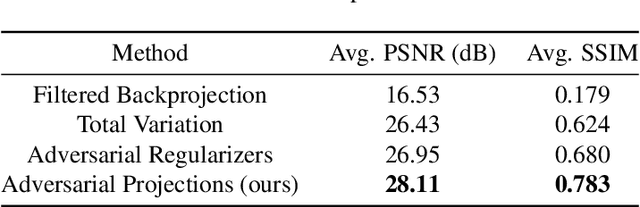
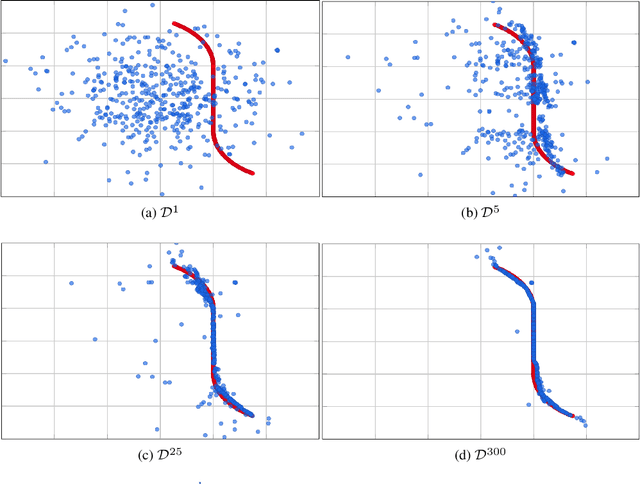
We present a new framework, called adversarial projections, for solving inverse problems by learning to project onto manifolds. Our goal is to recover a signal from a collection of noisy measurements. Traditional methods for this task often minimize the addition of a regularization term and an expression that measures compliance with measurements (e.g., least squares). However, it has been shown that convex regularization can introduce bias, preventing recovery of the true signal. Our approach avoids this issue by iteratively projecting signals toward the (possibly nonlinear) manifold of true signals. This is accomplished by first solving a sequence of unsupervised learning problems. The solution to each learning problem provides a collection of parameters that enables access to an iteration-dependent step size and access to the direction to project each signal toward the closest true signal. Given a signal estimate (e.g., recovered from a pseudo-inverse), we prove our method generates a sequence that converges in mean square to the projection onto this manifold. Several numerical illustrations are provided.