MS-IMAP -- A Multi-Scale Graph Embedding Approach for Interpretable Manifold Learning

Deriving meaningful representations from complex, high-dimensional data in unsupervised settings is crucial across diverse machine learning applications. This paper introduces a framework for multi-scale graph network embedding based on spectral graph wavelets that employs a contrastive learning approach. A significant feature of the proposed embedding is its capacity to establish a correspondence between the embedding space and the input feature space which aids in deriving feature importance of the original features. We theoretically justify our approach and demonstrate that, in Paley-Wiener spaces on combinatorial graphs, the spectral graph wavelets operator offers greater flexibility and better control over smoothness properties compared to the Laplacian operator. We validate the effectiveness of our proposed graph embedding on a variety of public datasets through a range of downstream tasks, including clustering and unsupervised feature importance.

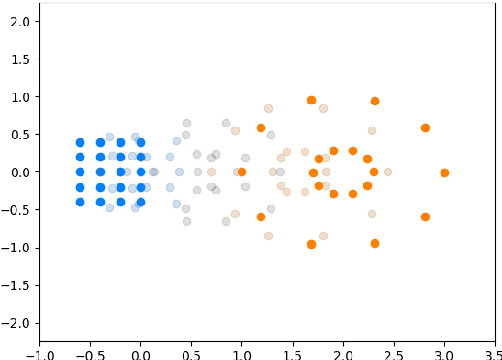
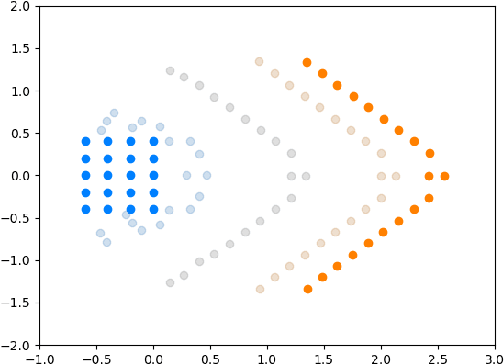
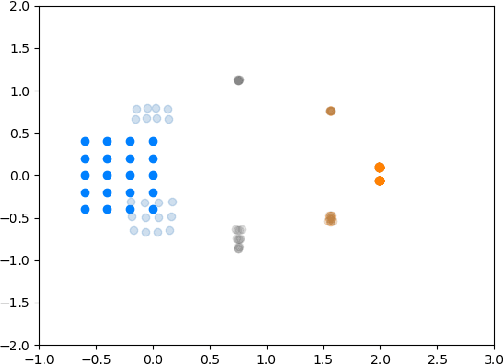
Multi-Agent Shape Control with Optimal Transport

We introduce a method called MASCOT (Multi-Agent Shape Control with Optimal Transport) to compute optimal control solutions of agents with shape/formation/density constraints. For example, we might want to apply shape constraints on the agents -- perhaps we desire the agents to hold a particular shape along the path, or we want agents to spread out in order to minimize collisions. We might also want a proportion of agents to move to one destination, while the other agents move to another, and to do this in the optimal way, i.e. the source-destination assignments should be optimal. In order to achieve this, we utilize the Earth Mover's Distance from Optimal Transport to distribute the agents into their proper positions so that certain shapes can be satisfied. This cost is both introduced in the terminal cost and in the running cost of the optimal control problem.

Parameter Inference of Time Series by Delay Embeddings and Learning Differentiable Operators

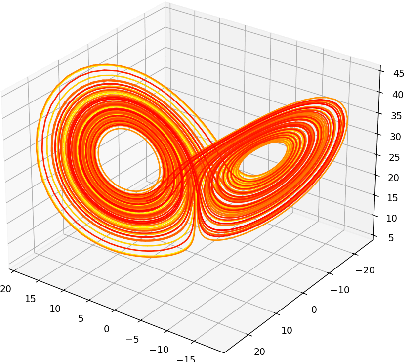
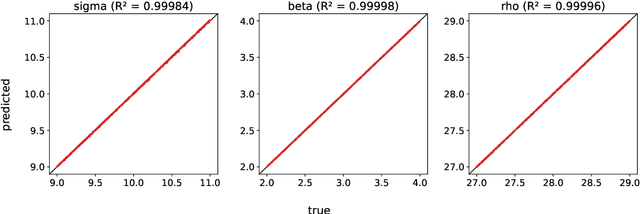
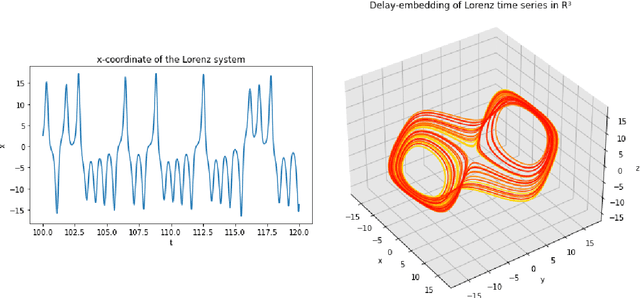
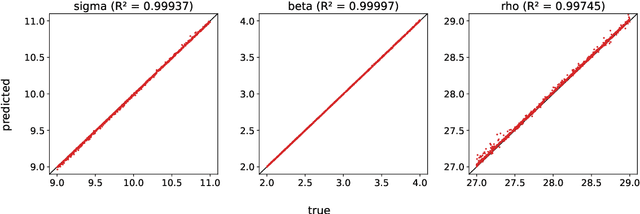
A common issue in dealing with real-world dynamical systems is identifying system parameters responsible for its behavior. A frequent scenario is that one has time series data, along with corresponding parameter labels, but there exists new time series with unknown parameter labels, which one seeks to identify. We tackle this problem by first delay-embedding the time series into a higher dimension to obtain a proper ordinary differential equation (ODE), and then having a neural network learn to predict future time-steps of the trajectory given the present time-step. We then use the learned neural network to backpropagate prediction errors through the parameter inputs of the neural network in order to obtain a gradient in parameter space. Using this gradient, we can approximately identify parameters of time series. We demonstrate the viability of our approach on the chaotic Lorenz system, as well as real-world data with the Hall-effect Thruster (HET).

Wasserstein Proximal of GANs

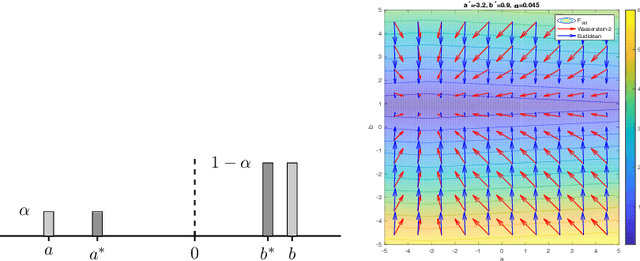
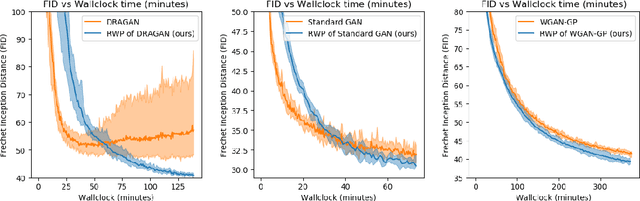
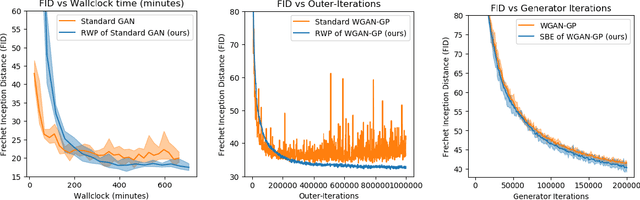
We introduce a new method for training generative adversarial networks by applying the Wasserstein-2 metric proximal on the generators. The approach is based on Wasserstein information geometry. It defines a parametrization invariant natural gradient by pulling back optimal transport structures from probability space to parameter space. We obtain easy-to-implement iterative regularizers for the parameter updates of implicit deep generative models. Our experiments demonstrate that this method improves the speed and stability of training in terms of wall-clock time and Fr\'echet Inception Distance.

Projecting to Manifolds via Unsupervised Learning

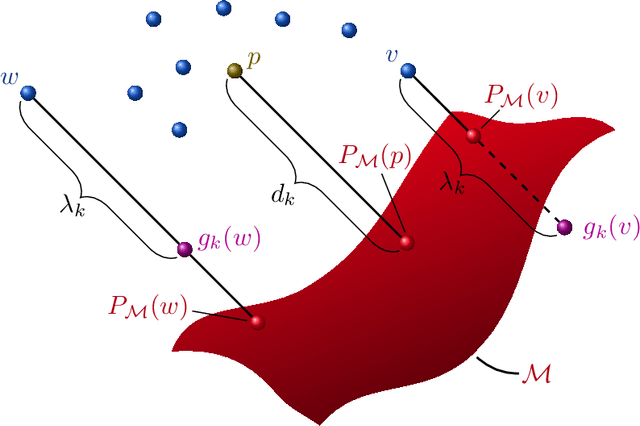
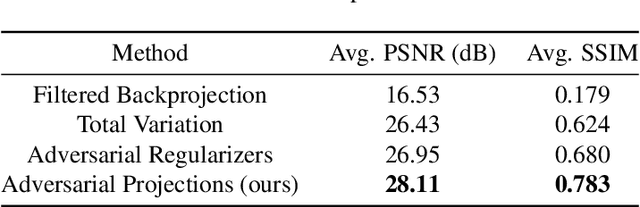
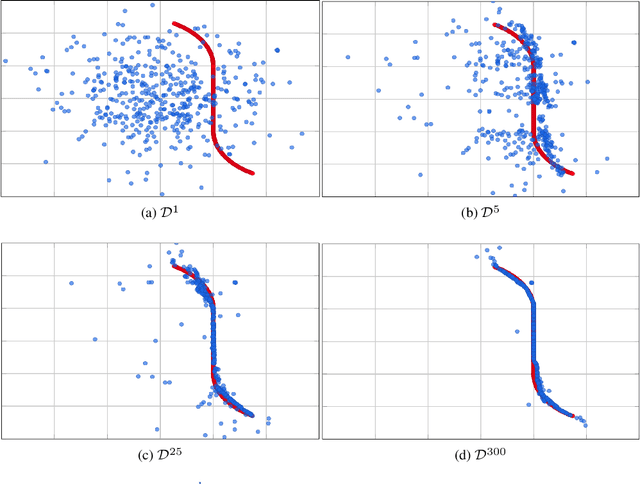
We present a new framework, called adversarial projections, for solving inverse problems by learning to project onto manifolds. Our goal is to recover a signal from a collection of noisy measurements. Traditional methods for this task often minimize the addition of a regularization term and an expression that measures compliance with measurements (e.g., least squares). However, it has been shown that convex regularization can introduce bias, preventing recovery of the true signal. Our approach avoids this issue by iteratively projecting signals toward the (possibly nonlinear) manifold of true signals. This is accomplished by first solving a sequence of unsupervised learning problems. The solution to each learning problem provides a collection of parameters that enables access to an iteration-dependent step size and access to the direction to project each signal toward the closest true signal. Given a signal estimate (e.g., recovered from a pseudo-inverse), we prove our method generates a sequence that converges in mean square to the projection onto this manifold. Several numerical illustrations are provided.

APAC-Net: Alternating the Population and Agent Control via Two Neural Networks to Solve High-Dimensional Stochastic Mean Field Games

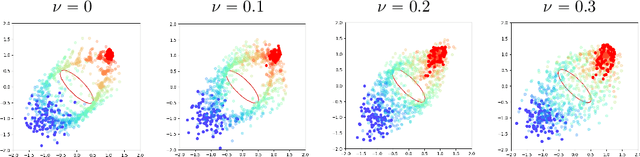
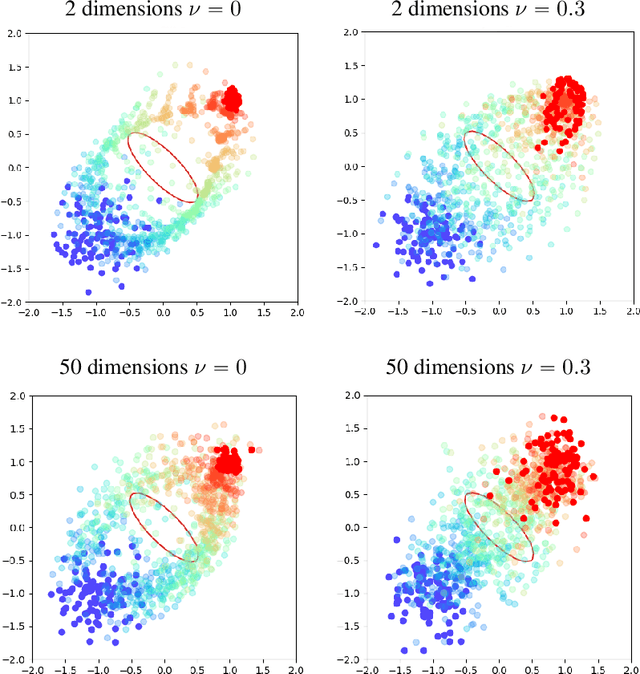
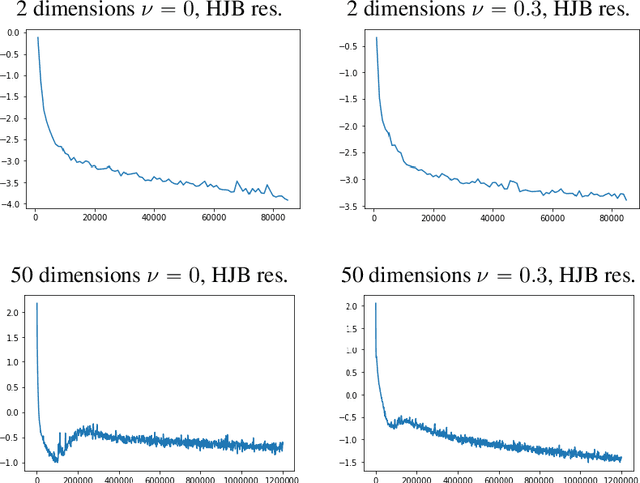
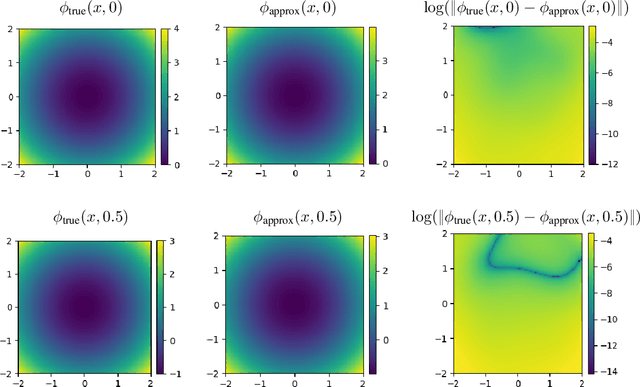
We present APAC-Net, an alternating population and agent control neural network for solving stochastic mean field games (MFGs). Our algorithm is geared toward high-dimensional instances MFGs that are beyond reach with existing solution methods. We achieve this in two steps. First, we take advantage of the underlying variational primal-dual structure that MFGs exhibit and phrase it as a convex-concave saddle point problem. Second, we parameterize the value and density functions by two neural networks, respectively. By phrasing the problem in this manner, solving the MFG can be interpreted as a special case of training a generative adversarial generative network (GAN). We show the potential of our method on up to 50-dimensional MFG problems.

Wasserstein Diffusion Tikhonov Regularization

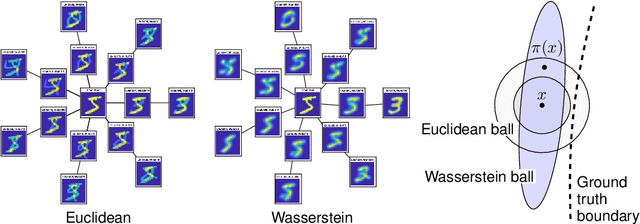
We propose regularization strategies for learning discriminative models that are robust to in-class variations of the input data. We use the Wasserstein-2 geometry to capture semantically meaningful neighborhoods in the space of images, and define a corresponding input-dependent additive noise data augmentation model. Expanding and integrating the augmented loss yields an effective Tikhonov-type Wasserstein diffusion smoothness regularizer. This approach allows us to apply high levels of regularization and train functions that have low variability within classes but remain flexible across classes. We provide efficient methods for computing the regularizer at a negligible cost in comparison to training with adversarial data augmentation. Initial experiments demonstrate improvements in generalization performance under adversarial perturbations and also large in-class variations of the input data.

CESMA: Centralized Expert Supervises Multi-Agents

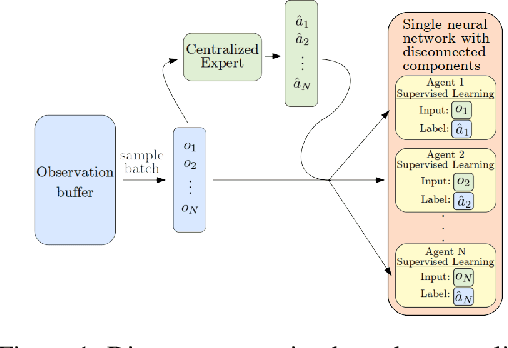
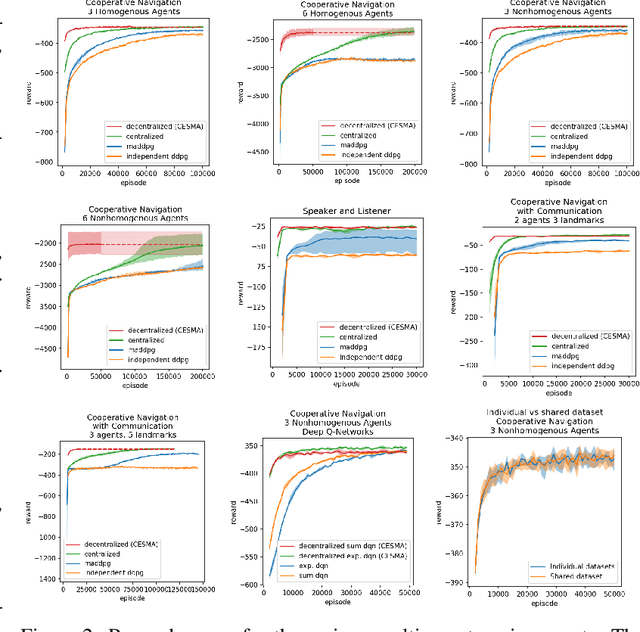
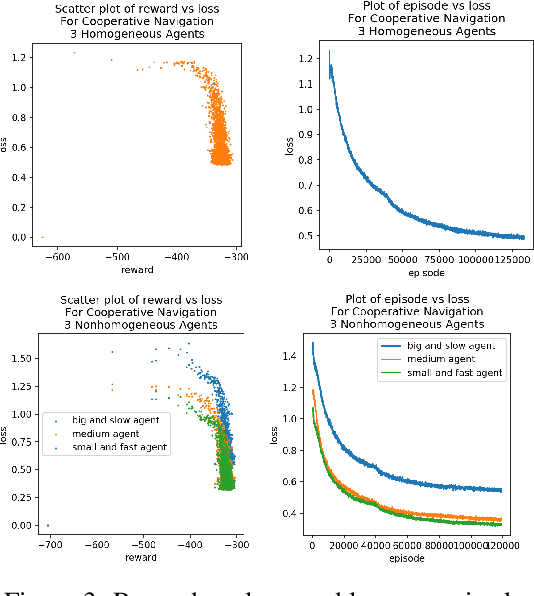
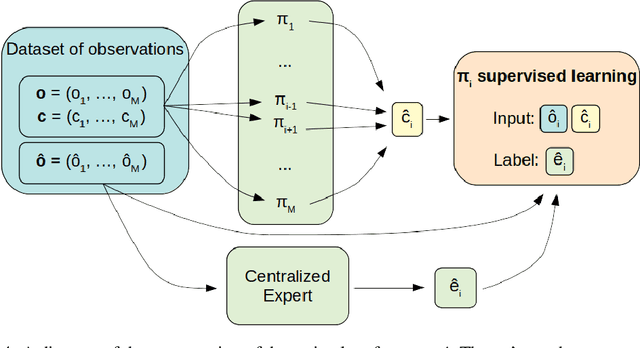
We consider the reinforcement learning problem of training multiple agents in order to maximize a shared reward. In this multi-agent system, each agent seeks to maximize the reward while interacting with other agents, and they may or may not be able to communicate. Typically the agents do not have access to other agent policies and thus each agent observes a non-stationary and partially-observable environment. In order to resolve this issue, we demonstrate a novel multi-agent training framework that first turns a multi-agent problem into a single-agent problem to obtain a centralized expert that is then used to guide supervised learning for multiple independent agents with the goal of decentralizing the policy. We additionally demonstrate a way to turn the exponential growth in the joint action space into a linear growth for the centralized policy. Overall, the problem is twofold: the problem of obtaining a centralized expert, and then the problem of supervised learning to train the multi-agents. We demonstrate our solutions to both of these tasks, and show that supervised learning can be used to decentralize a multi-agent policy.