MS-IMAP -- A Multi-Scale Graph Embedding Approach for Interpretable Manifold Learning

Deriving meaningful representations from complex, high-dimensional data in unsupervised settings is crucial across diverse machine learning applications. This paper introduces a framework for multi-scale graph network embedding based on spectral graph wavelets that employs a contrastive learning approach. A significant feature of the proposed embedding is its capacity to establish a correspondence between the embedding space and the input feature space which aids in deriving feature importance of the original features. We theoretically justify our approach and demonstrate that, in Paley-Wiener spaces on combinatorial graphs, the spectral graph wavelets operator offers greater flexibility and better control over smoothness properties compared to the Laplacian operator. We validate the effectiveness of our proposed graph embedding on a variety of public datasets through a range of downstream tasks, including clustering and unsupervised feature importance.

Graph Spectral Embedding using the Geodesic Betweeness Centrality

We introduce the Graph Sylvester Embedding (GSE), an unsupervised graph representation of local similarity, connectivity, and global structure. GSE uses the solution of the Sylvester equation to capture both network structure and neighborhood proximity in a single representation. Unlike embeddings based on the eigenvectors of the Laplacian, GSE incorporates two or more basis functions, for instance using the Laplacian and the affinity matrix. Such basis functions are constructed not from the original graph, but from one whose weights measure the centrality of an edge (the fraction of the number of shortest paths that pass through that edge) in the original graph. This allows more flexibility and control to represent complex network structure and shows significant improvements over the state of the art when used for data analysis tasks such as predicting failed edges in material science and network alignment in the human-SARS CoV-2 protein-protein interactome.

Spectral Embedding of Graph Networks

We introduce an unsupervised graph embedding that trades off local node similarity and connectivity, and global structure. The embedding is based on a generalized graph Laplacian, whose eigenvectors compactly capture both network structure and neighborhood proximity in a single representation. The key idea is to transform the given graph into one whose weights measure the centrality of an edge by the fraction of the number of shortest paths that pass through that edge, and employ its spectral proprieties in the representation. Testing the resulting graph network representation shows significant improvement over the sate of the art in data analysis tasks including social networks and material science. We also test our method on node classification from the human-SARS CoV-2 protein-protein interactome.

Zero Shot Learning with the Isoperimetric Loss

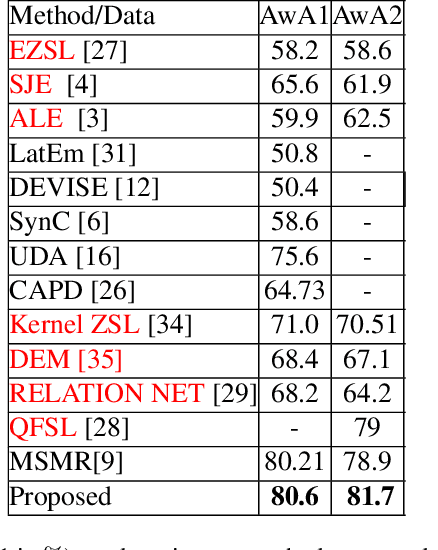
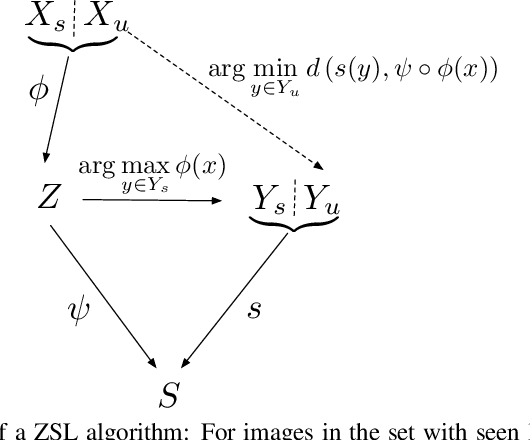
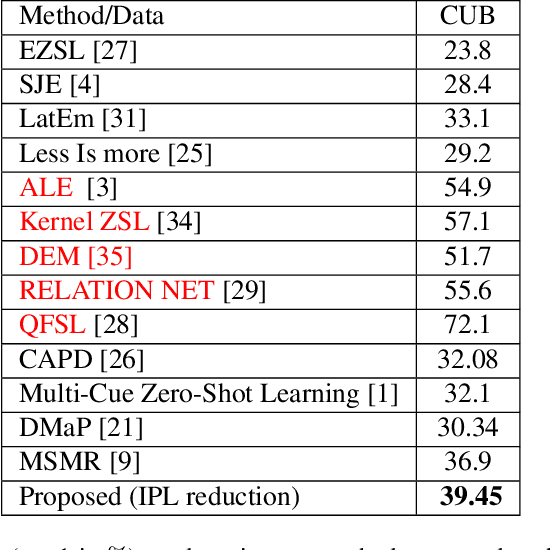
We introduce the isoperimetric loss as a regularization criterion for learning the map from a visual representation to a semantic embedding, to be used to transfer knowledge to unknown classes in a zero-shot learning setting. We use a pre-trained deep neural network model as a visual representation of image data, a Word2Vec embedding of class labels, and linear maps between the visual and semantic embedding spaces. However, the spaces themselves are not linear, and we postulate the sample embedding to be populated by noisy samples near otherwise smooth manifolds. We exploit the graph structure defined by the sample points to regularize the estimates of the manifolds by inferring the graph connectivity using a generalization of the isoperimetric inequalities from Riemannian geometry to graphs. Surprisingly, this regularization alone, paired with the simplest baseline model, outperforms the state-of-the-art among fully automated methods in zero-shot learning benchmarks such as AwA and CUB. This improvement is achieved solely by learning the structure of the underlying spaces by imposing regularity.

Graph-Based Manifold Frequency Analysis for Denoising

We propose a new framework for manifold denoising based on processing in the graph Fourier frequency domain, derived from the spectral decomposition of the discrete graph Laplacian. Our approach uses the Spectral Graph Wavelet transform in order to per- form non-iterative denoising directly in the graph frequency domain, an approach inspired by conventional wavelet-based signal denoising methods. We theoretically justify our approach, based on the fact that for smooth manifolds the coordinate information energy is localized in the low spectral graph wavelet sub-bands, while the noise affects all frequency bands in a similar way. Experimental results show that our proposed manifold frequency denoising (MFD) approach significantly outperforms the state of the art denoising meth- ods, and is robust to a wide range of parameter selections, e.g., the choice of k nearest neighbor connectivity of the graph.