MS-IMAP -- A Multi-Scale Graph Embedding Approach for Interpretable Manifold Learning

Deriving meaningful representations from complex, high-dimensional data in unsupervised settings is crucial across diverse machine learning applications. This paper introduces a framework for multi-scale graph network embedding based on spectral graph wavelets that employs a contrastive learning approach. A significant feature of the proposed embedding is its capacity to establish a correspondence between the embedding space and the input feature space which aids in deriving feature importance of the original features. We theoretically justify our approach and demonstrate that, in Paley-Wiener spaces on combinatorial graphs, the spectral graph wavelets operator offers greater flexibility and better control over smoothness properties compared to the Laplacian operator. We validate the effectiveness of our proposed graph embedding on a variety of public datasets through a range of downstream tasks, including clustering and unsupervised feature importance.

Agglomerative Fast Super-Paramagnetic Clustering

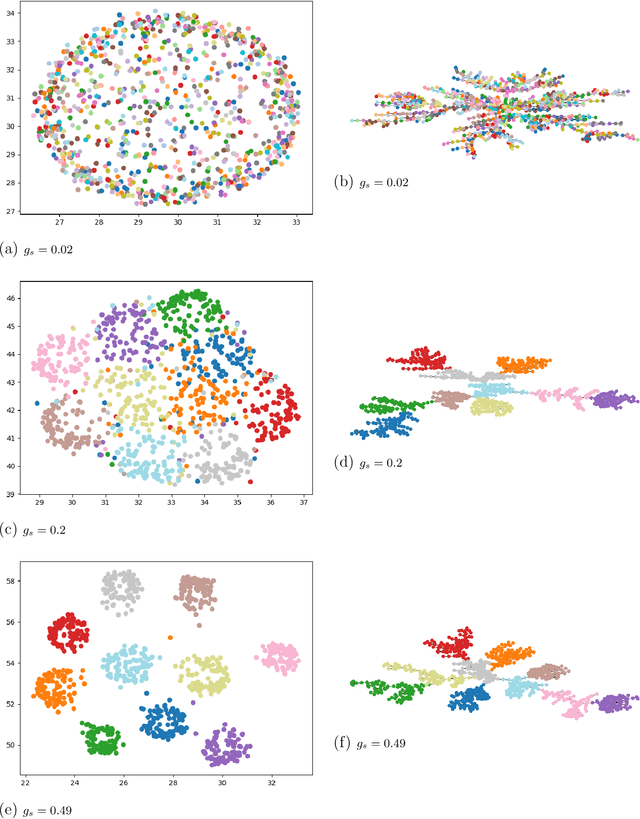
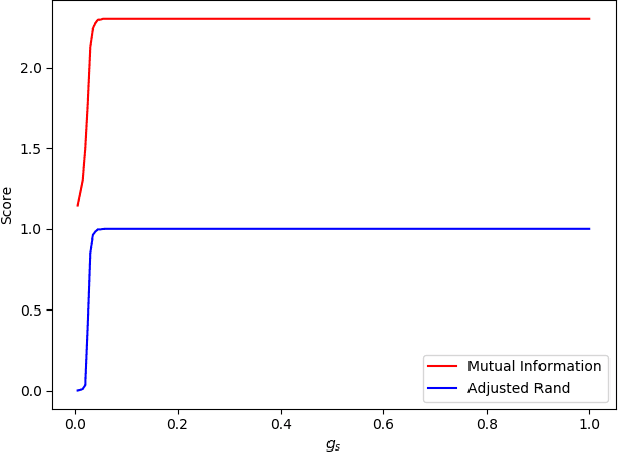
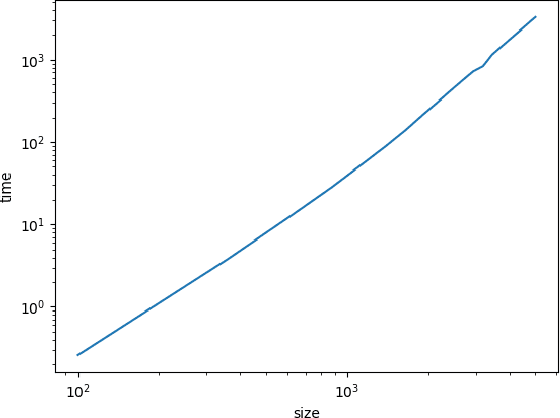
We consider the problem of fast time-series data clustering. Building on previous work modeling the correlation-based Hamiltonian of spin variables we present a fast non-expensive agglomerative algorithm. The method is tested on synthetic correlated time-series and noisy synthetic data-sets with built-in cluster structure to demonstrate that the algorithm produces meaningful non-trivial results. We argue that ASPC can reduce compute time costs and resource usage cost for large scale clustering while being serialized and hence has no obvious parallelization requirement. The algorithm can be an effective choice for state-detection for online learning in a fast non-linear data environment because the algorithm requires no prior information about the number of clusters.