Parameter Inference of Time Series by Delay Embeddings and Learning Differentiable Operators

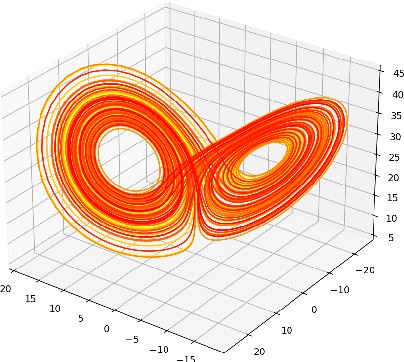
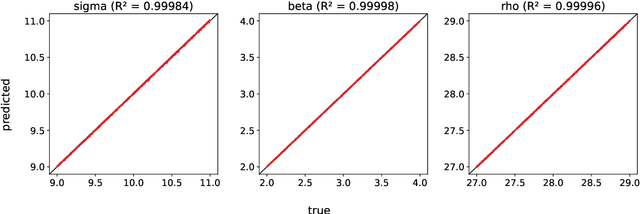
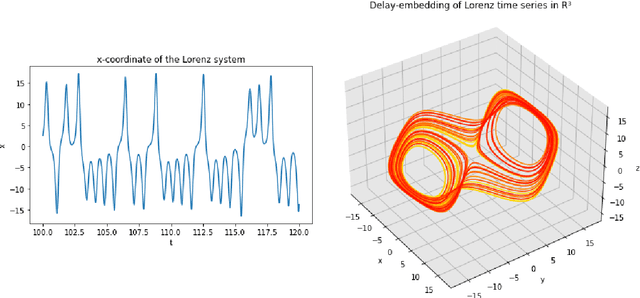
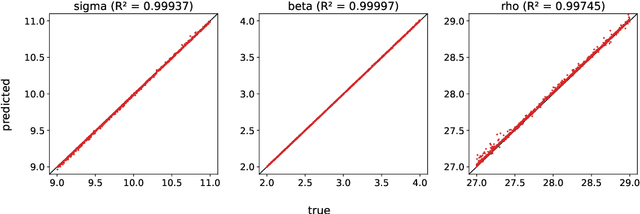
A common issue in dealing with real-world dynamical systems is identifying system parameters responsible for its behavior. A frequent scenario is that one has time series data, along with corresponding parameter labels, but there exists new time series with unknown parameter labels, which one seeks to identify. We tackle this problem by first delay-embedding the time series into a higher dimension to obtain a proper ordinary differential equation (ODE), and then having a neural network learn to predict future time-steps of the trajectory given the present time-step. We then use the learned neural network to backpropagate prediction errors through the parameter inputs of the neural network in order to obtain a gradient in parameter space. Using this gradient, we can approximately identify parameters of time series. We demonstrate the viability of our approach on the chaotic Lorenz system, as well as real-world data with the Hall-effect Thruster (HET).