Mark J. Debord
A Hamilton-Jacobi Formulation for Optimal Coordination of Heterogeneous Multiple Vehicle Systems
Mar 12, 2020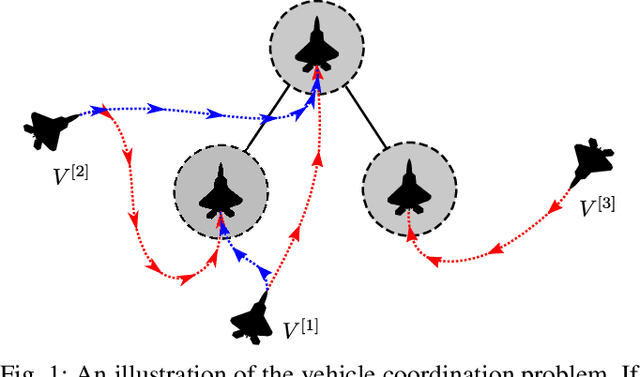
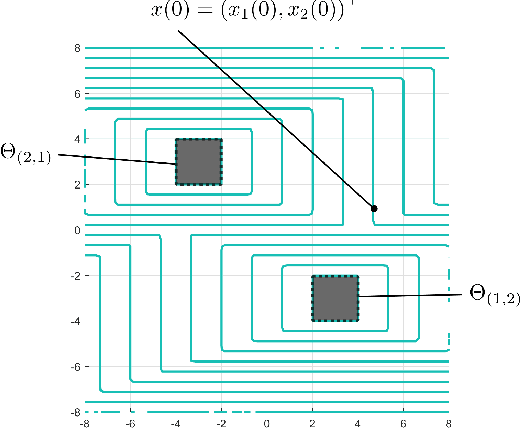
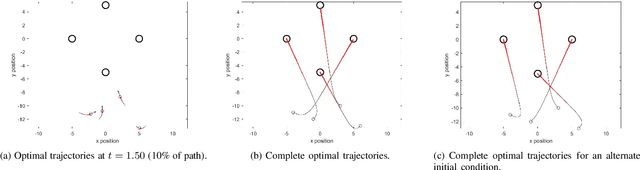
Abstract:We present a method for optimal coordination of multiple vehicle teams when multiple endpoint configurations are equally desirable, such as seen in the autonomous assembly of formation flight. The individual vehicles' positions in the formation are not assigned a priori and a key challenge is to find the optimal configuration assignment along with the optimal control and trajectory. Commonly, assignment and trajectory planning problems are solved separately. We introduce a new multi-vehicle coordination paradigm, where the optimal goal assignment and optimal vehicle trajectories are found simultaneously from a viscosity solution of a single Hamilton-Jacobi (HJ) partial differential equation (PDE), which provides a necessary and sufficient condition for global optimality. Intrinsic in this approach is that individual vehicle dynamic models need not be the same, and therefore can be applied to heterogeneous systems. Numerical methods to solve the HJ equation have historically relied on a discrete grid of the solution space and exhibits exponential scaling with system dimension, preventing their applicability to multiple vehicle systems. By utilizing a generalization of the Hopf formula, we avoid the use of grids and present a method that exhibits polynomial scaling in the number of vehicles.
CESMA: Centralized Expert Supervises Multi-Agents
Feb 07, 2019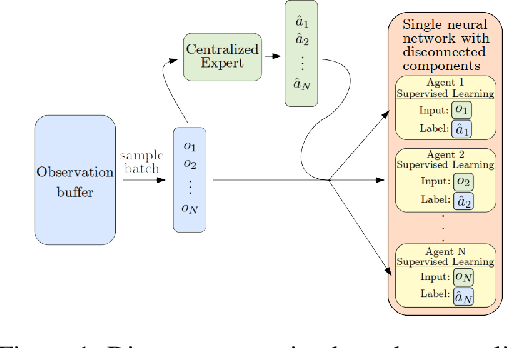
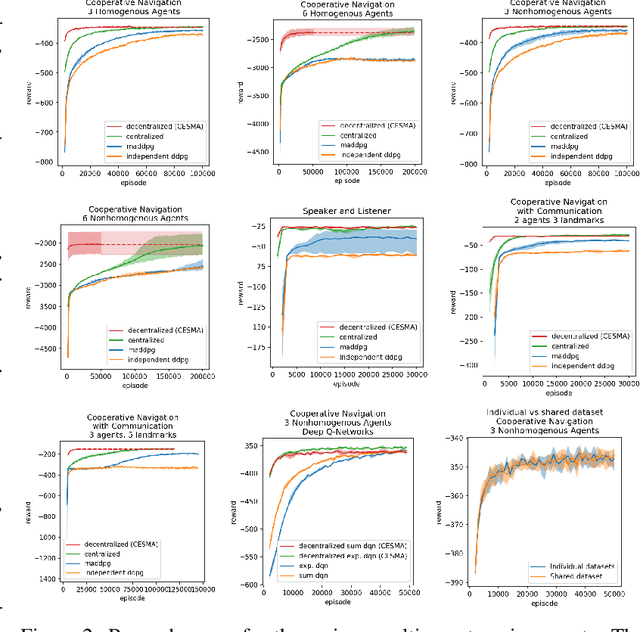
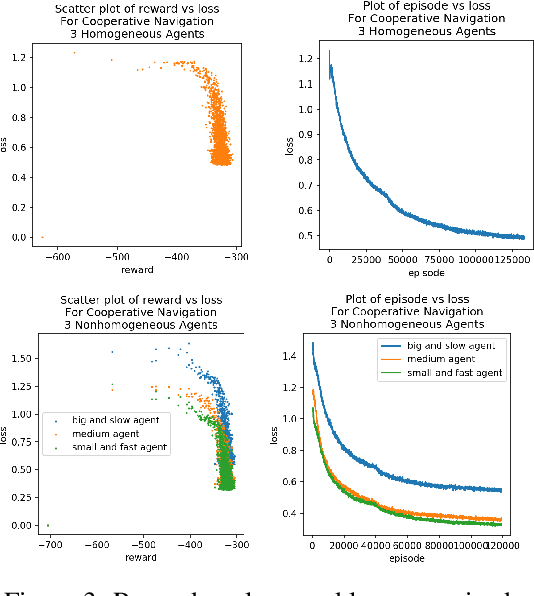
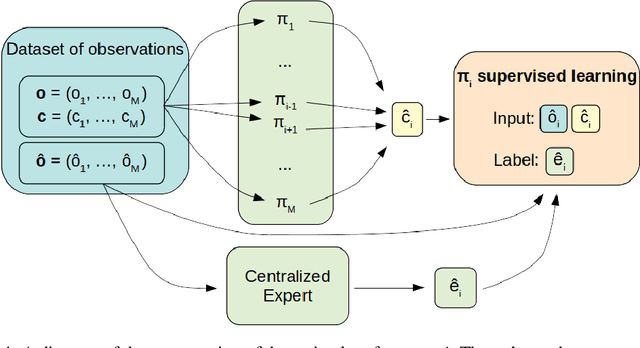
Abstract:We consider the reinforcement learning problem of training multiple agents in order to maximize a shared reward. In this multi-agent system, each agent seeks to maximize the reward while interacting with other agents, and they may or may not be able to communicate. Typically the agents do not have access to other agent policies and thus each agent observes a non-stationary and partially-observable environment. In order to resolve this issue, we demonstrate a novel multi-agent training framework that first turns a multi-agent problem into a single-agent problem to obtain a centralized expert that is then used to guide supervised learning for multiple independent agents with the goal of decentralizing the policy. We additionally demonstrate a way to turn the exponential growth in the joint action space into a linear growth for the centralized policy. Overall, the problem is twofold: the problem of obtaining a centralized expert, and then the problem of supervised learning to train the multi-agents. We demonstrate our solutions to both of these tasks, and show that supervised learning can be used to decentralize a multi-agent policy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge