Trajectories for the Optimal Collection of Information

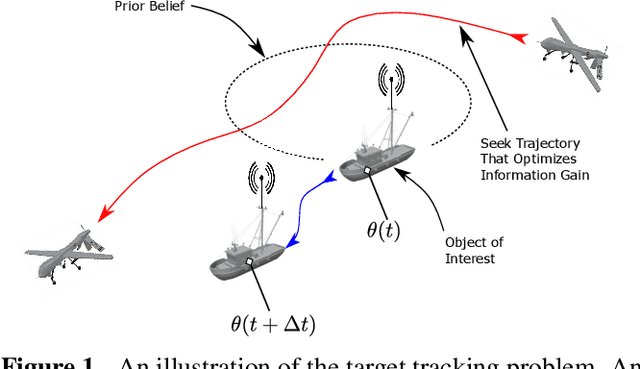
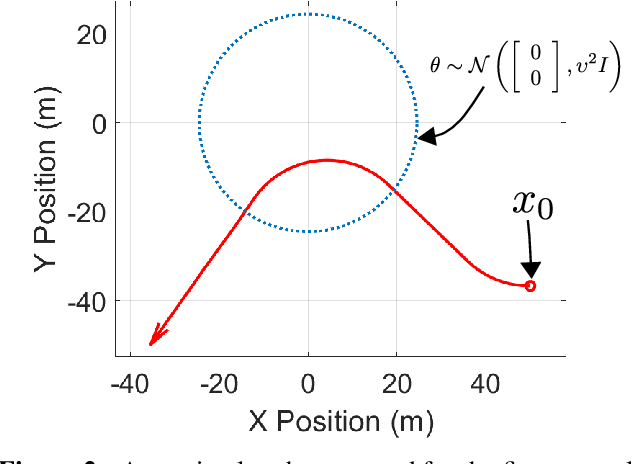
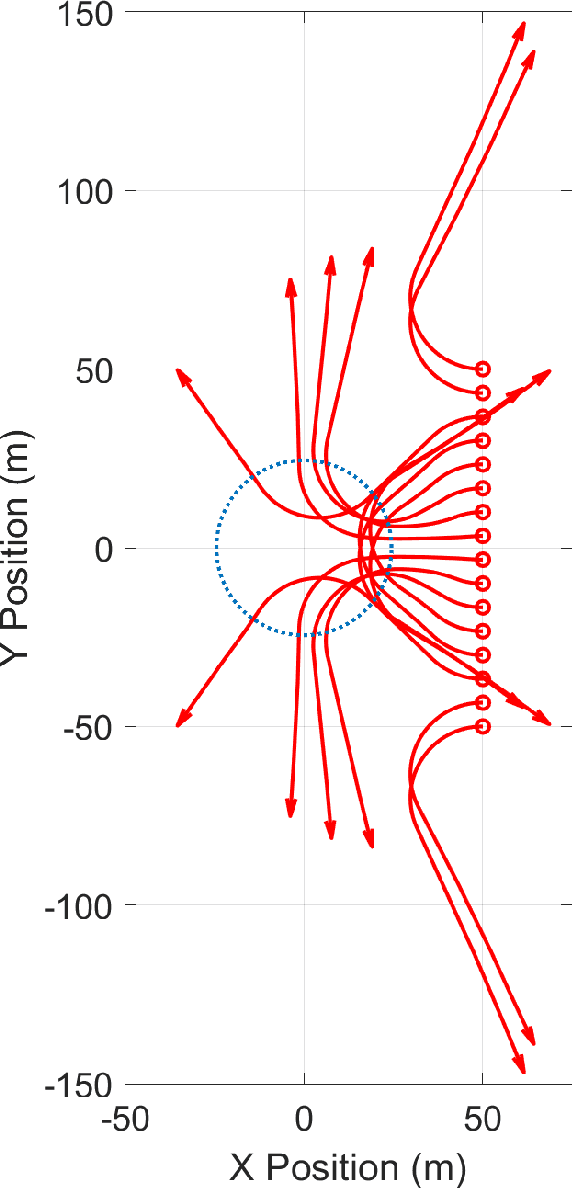
We study a scenario where an aircraft has multiple heterogeneous sensors collecting measurements to track a target vehicle of unknown location. The measurements are sampled along the flight path and our goals to optimize sensor placement to minimize estimation error. We select as a metric the Fisher Information Matrix (FIM), as "minimizing" the inverse of the FIM is required to achieve small estimation error. We propose to generate the optimal path from the Hamilton-Jacobi (HJ) partial differential equation (PDE) as it is the necessary and sufficient condition for optimality. A traditional method of lines (MOL) approach, based on a spatial grid, lends itself well to the highly non-linear and non-convex structure of the problem induced by the FIM matrix. However, the sensor placement problem results in a state space dimension that renders a naive MOL approach intractable. We present a new hybrid approach, whereby we decompose the state space into two parts: a smaller subspace that still uses a grid and takes advantage of the robustness to non-linearities and non-convexities, and the remaining state space that can by found efficiently from a system of ODEs, avoiding formation of a spatial grid.

Reachability as a Unifying Framework for Computing Helicopter Safe Operating Conditions and Autonomous Emergency Landing

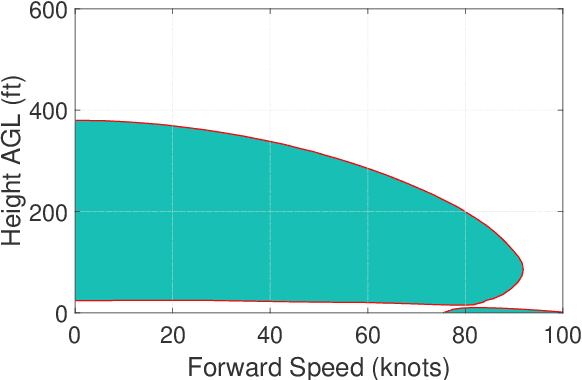
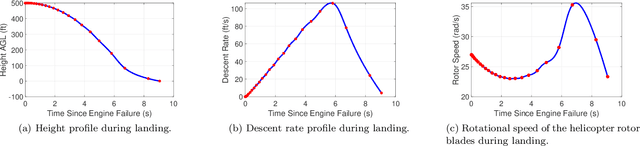
We present a numeric method to compute the safe operating flight conditions for a helicopter such that we can ensure a safe landing in the event of a partial or total engine failure. The unsafe operating region is the complement of the backwards reachable tube, which can be found as the sub-zero level set of the viscosity solution of a Hamilton-Jacobi (HJ) equation. Traditionally, numerical methods used to solve the HJ equation rely on a discrete grid of the solution space and exhibit exponential scaling with dimension, which is problematic for the high-fidelity dynamics models required for accurate helicopter modeling. We avoid the use of spatial grids by formulating a trajectory optimization problem, where the solution at each initial condition can be computed in a computationally efficient manner. The proposed method is shown to compute an autonomous landing trajectory from any operating condition, even in non-cruise flight conditions.

A Hamilton-Jacobi Formulation for Optimal Coordination of Heterogeneous Multiple Vehicle Systems

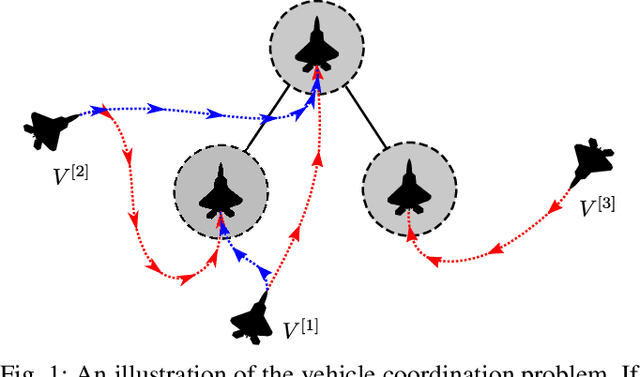
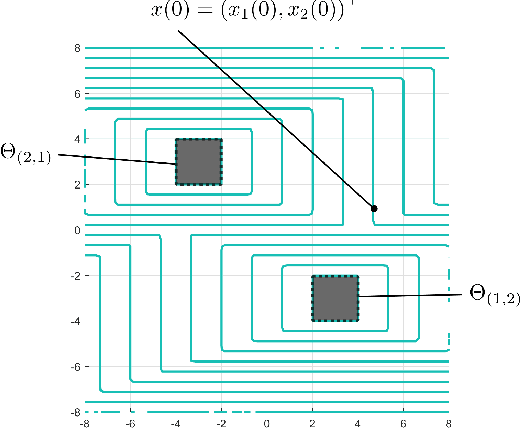
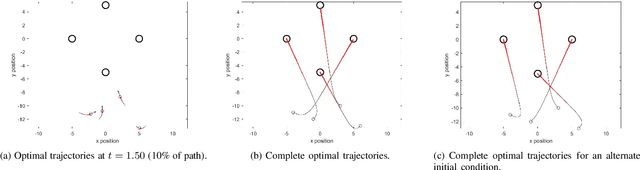
We present a method for optimal coordination of multiple vehicle teams when multiple endpoint configurations are equally desirable, such as seen in the autonomous assembly of formation flight. The individual vehicles' positions in the formation are not assigned a priori and a key challenge is to find the optimal configuration assignment along with the optimal control and trajectory. Commonly, assignment and trajectory planning problems are solved separately. We introduce a new multi-vehicle coordination paradigm, where the optimal goal assignment and optimal vehicle trajectories are found simultaneously from a viscosity solution of a single Hamilton-Jacobi (HJ) partial differential equation (PDE), which provides a necessary and sufficient condition for global optimality. Intrinsic in this approach is that individual vehicle dynamic models need not be the same, and therefore can be applied to heterogeneous systems. Numerical methods to solve the HJ equation have historically relied on a discrete grid of the solution space and exhibits exponential scaling with system dimension, preventing their applicability to multiple vehicle systems. By utilizing a generalization of the Hopf formula, we avoid the use of grids and present a method that exhibits polynomial scaling in the number of vehicles.

Automatic Thresholding of SIFT Descriptors

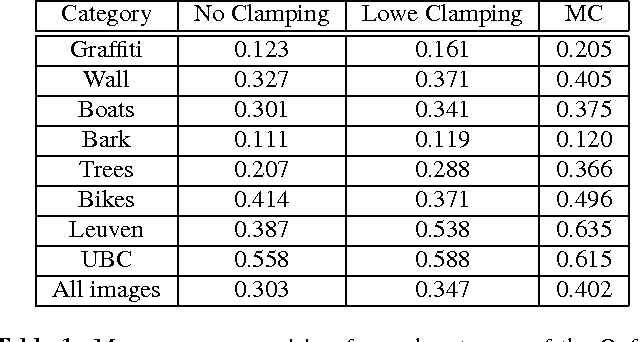
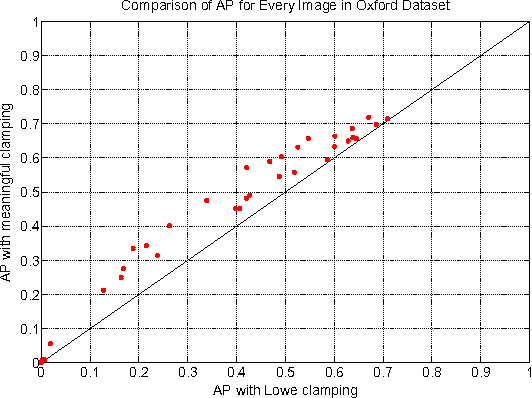
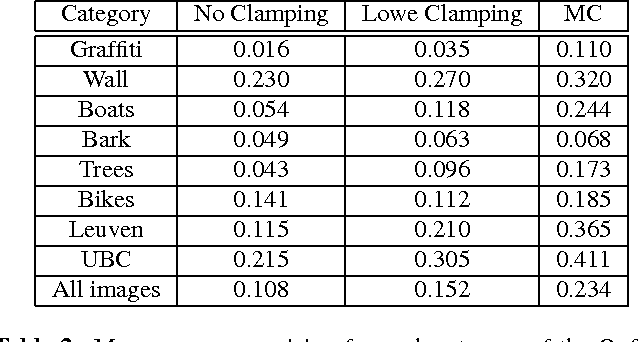
We introduce a method to perform automatic thresholding of SIFT descriptors that improves matching performance by at least 15.9% on the Oxford image matching benchmark. The method uses a contrario methodology to determine a unique bin magnitude threshold. This is done by building a generative uniform background model for descriptors and determining when bin magnitudes have reached a sufficient level. The presented method, called meaningful clamping, contrasts from the current SIFT implementation by efficiently computing a clamping threshold that is unique for every descriptor.