RoSSO: A High-Performance Python Package for Robotic Surveillance Strategy Optimization Using JAX

To enable the computation of effective randomized patrol routes for single- or multi-robot teams, we present RoSSO, a Python package designed for solving Markov chain optimization problems. We exploit machine-learning techniques such as reverse-mode automatic differentiation and constraint parametrization to achieve superior efficiency compared to general-purpose nonlinear programming solvers. Additionally, we supplement a game-theoretic stochastic surveillance formulation in the literature with a novel greedy algorithm and multi-robot extension. We close with numerical results for a police district in downtown San Francisco that demonstrate RoSSO's capabilities on our new formulations and the prior work.

Trajectories for the Optimal Collection of Information

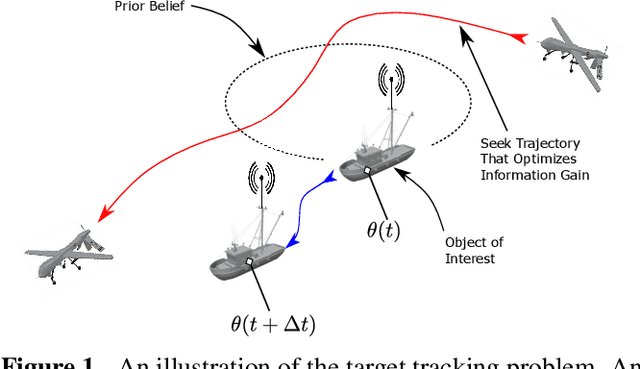
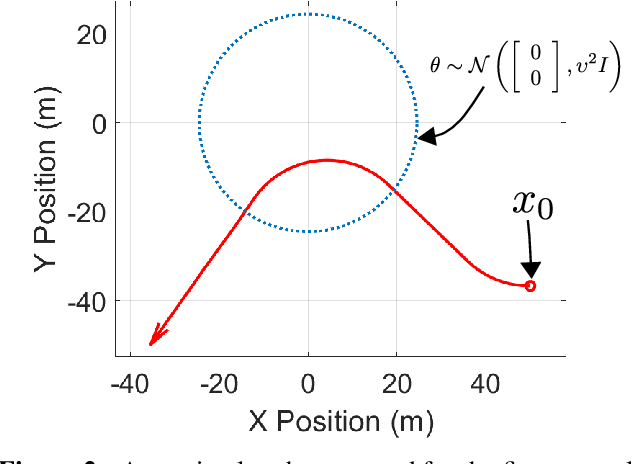
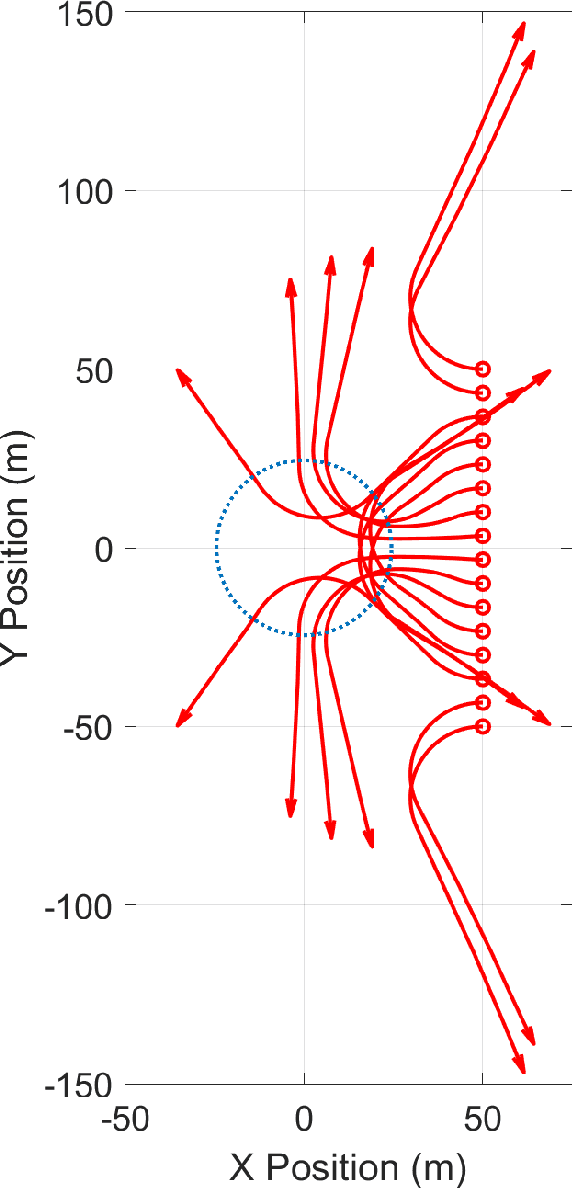
We study a scenario where an aircraft has multiple heterogeneous sensors collecting measurements to track a target vehicle of unknown location. The measurements are sampled along the flight path and our goals to optimize sensor placement to minimize estimation error. We select as a metric the Fisher Information Matrix (FIM), as "minimizing" the inverse of the FIM is required to achieve small estimation error. We propose to generate the optimal path from the Hamilton-Jacobi (HJ) partial differential equation (PDE) as it is the necessary and sufficient condition for optimality. A traditional method of lines (MOL) approach, based on a spatial grid, lends itself well to the highly non-linear and non-convex structure of the problem induced by the FIM matrix. However, the sensor placement problem results in a state space dimension that renders a naive MOL approach intractable. We present a new hybrid approach, whereby we decompose the state space into two parts: a smaller subspace that still uses a grid and takes advantage of the robustness to non-linearities and non-convexities, and the remaining state space that can by found efficiently from a system of ODEs, avoiding formation of a spatial grid.

Policy Evaluation and Seeking for Multi-Agent Reinforcement Learning via Best Response

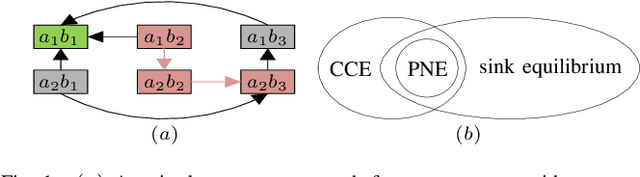
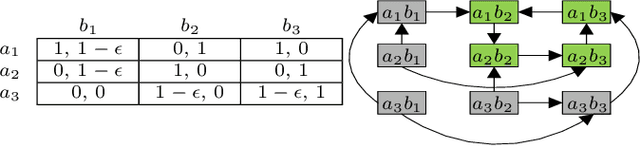
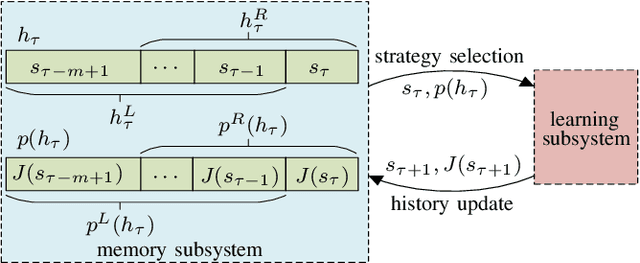
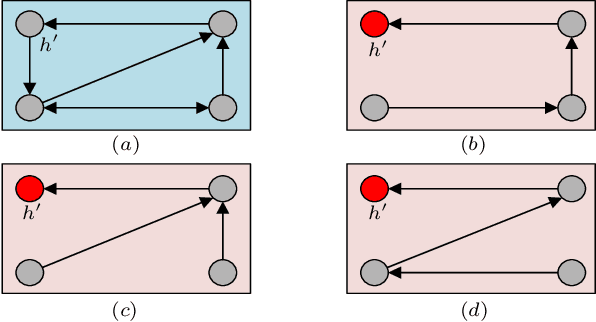
This paper introduces two metrics (cycle-based and memory-based metrics), grounded on a dynamical game-theoretic solution concept called sink equilibrium, for the evaluation, ranking, and computation of policies in multi-agent learning. We adopt strict best response dynamics (SBRD) to model selfish behaviors at a meta-level for multi-agent reinforcement learning. Our approach can deal with dynamical cyclical behaviors (unlike approaches based on Nash equilibria and Elo ratings), and is more compatible with single-agent reinforcement learning than alpha-rank which relies on weakly better responses. We first consider settings where the difference between largest and second largest underlying metric has a known lower bound. With this knowledge we propose a class of perturbed SBRD with the following property: only policies with maximum metric are observed with nonzero probability for a broad class of stochastic games with finite memory. We then consider settings where the lower bound for the difference is unknown. For this setting, we propose a class of perturbed SBRD such that the metrics of the policies observed with nonzero probability differ from the optimal by any given tolerance. The proposed perturbed SBRD addresses the opponent-induced non-stationarity by fixing the strategies of others for the learning agent, and uses empirical game-theoretic analysis to estimate payoffs for each strategy profile obtained due to the perturbation.