Multiplayer Homicidal Chauffeur Reach-Avoid Games: A Pursuit Enclosure Function Approach

This paper presents a multiplayer Homicidal Chauffeur reach-avoid differential game, which involves Dubins-car pursuers and simple-motion evaders. The goal of the pursuers is to cooperatively protect a planar convex region from the evaders, who strive to reach the region. We propose a cooperative strategy for the pursuers based on subgames for multiple pursuers against one evader and optimal task allocation. We introduce pursuit enclosure functions (PEFs) and propose a new enclosure region pursuit (ERP) winning approach that supports forward analysis for the strategy synthesis in the subgames. We show that if a pursuit coalition is able to defend the region against an evader under the ERP winning, then no more than two pursuers in the coalition are necessarily needed. We also propose a steer-to-ERP approach to certify the ERP winning and synthesize the ERP winning strategy. To implement the strategy, we introduce a positional PEF and provide the necessary parameters, states, and strategies that ensure the ERP winning for both one pursuer and two pursuers against one evader. Additionally, we formulate a binary integer program using the subgame outcomes to maximize the captured evaders in the ERP winning for the pursuit task allocation. Finally, we propose a multiplayer receding-horizon strategy where the ERP winnings are checked in each horizon, the task is allocated, and the strategies of the pursuers are determined. Numerical examples are provided to illustrate the results.

Policy Evaluation and Seeking for Multi-Agent Reinforcement Learning via Best Response

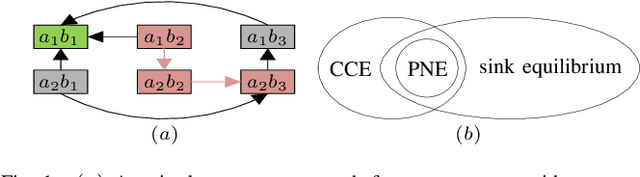
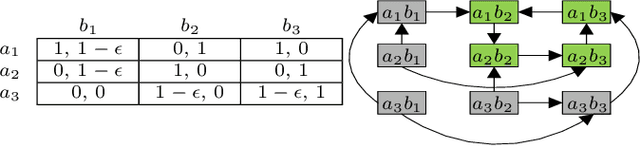
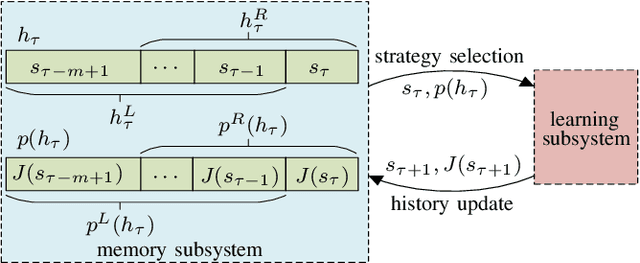
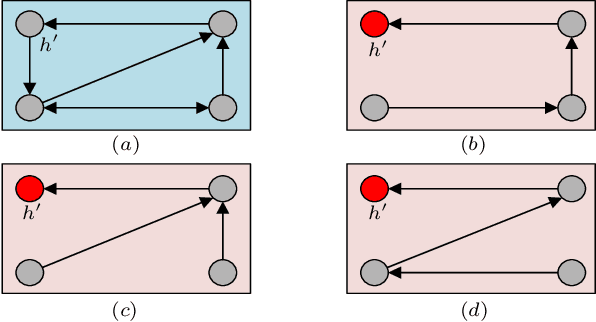
This paper introduces two metrics (cycle-based and memory-based metrics), grounded on a dynamical game-theoretic solution concept called sink equilibrium, for the evaluation, ranking, and computation of policies in multi-agent learning. We adopt strict best response dynamics (SBRD) to model selfish behaviors at a meta-level for multi-agent reinforcement learning. Our approach can deal with dynamical cyclical behaviors (unlike approaches based on Nash equilibria and Elo ratings), and is more compatible with single-agent reinforcement learning than alpha-rank which relies on weakly better responses. We first consider settings where the difference between largest and second largest underlying metric has a known lower bound. With this knowledge we propose a class of perturbed SBRD with the following property: only policies with maximum metric are observed with nonzero probability for a broad class of stochastic games with finite memory. We then consider settings where the lower bound for the difference is unknown. For this setting, we propose a class of perturbed SBRD such that the metrics of the policies observed with nonzero probability differ from the optimal by any given tolerance. The proposed perturbed SBRD addresses the opponent-induced non-stationarity by fixing the strategies of others for the learning agent, and uses empirical game-theoretic analysis to estimate payoffs for each strategy profile obtained due to the perturbation.