Learning Transferable Friction Models and LuGre Identification via Physics Informed Neural Networks

Accurately modeling friction in robotics remains a core challenge, as robotics simulators like Mujoco and PyBullet use simplified friction models or heuristics to balance computational efficiency with accuracy, where these simplifications and approximations can lead to substantial differences between simulated and physical performance. In this paper, we present a physics-informed friction estimation framework that enables the integration of well-established friction models with learnable components-requiring only minimal, generic measurement data. Our approach enforces physical consistency yet retains the flexibility to adapt to real-world complexities. We demonstrate, on an underactuated and nonlinear system, that the learned friction models, trained solely on small and noisy datasets, accurately simulate dynamic friction properties and reduce the sim-to-real gap. Crucially, we show that our approach enables the learned models to be transferable to systems they are not trained on. This ability to generalize across multiple systems streamlines friction modeling for complex, underactuated tasks, offering a scalable and interpretable path toward bridging the sim-to-real gap in robotics and control.

A Hamilton-Jacobi Formulation for Optimal Coordination of Heterogeneous Multiple Vehicle Systems

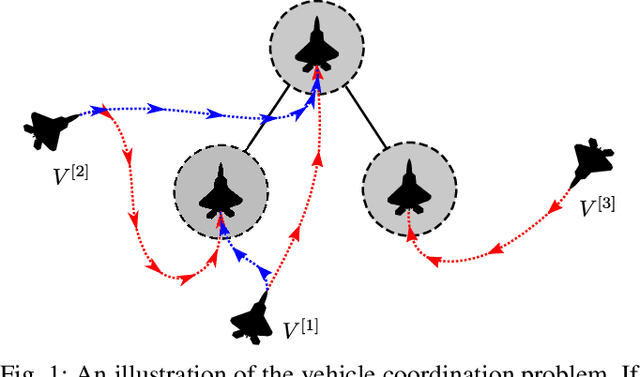
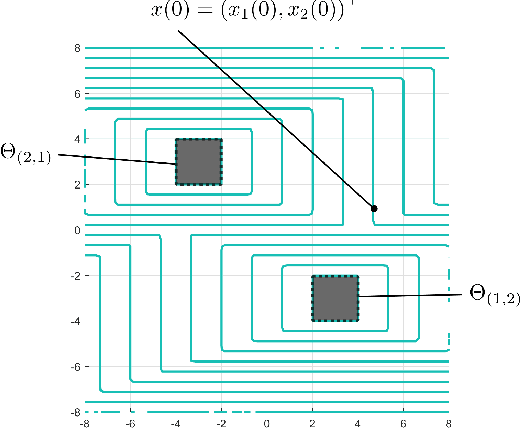
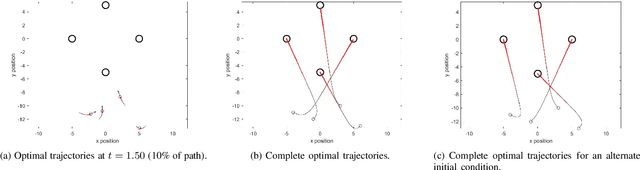
We present a method for optimal coordination of multiple vehicle teams when multiple endpoint configurations are equally desirable, such as seen in the autonomous assembly of formation flight. The individual vehicles' positions in the formation are not assigned a priori and a key challenge is to find the optimal configuration assignment along with the optimal control and trajectory. Commonly, assignment and trajectory planning problems are solved separately. We introduce a new multi-vehicle coordination paradigm, where the optimal goal assignment and optimal vehicle trajectories are found simultaneously from a viscosity solution of a single Hamilton-Jacobi (HJ) partial differential equation (PDE), which provides a necessary and sufficient condition for global optimality. Intrinsic in this approach is that individual vehicle dynamic models need not be the same, and therefore can be applied to heterogeneous systems. Numerical methods to solve the HJ equation have historically relied on a discrete grid of the solution space and exhibits exponential scaling with system dimension, preventing their applicability to multiple vehicle systems. By utilizing a generalization of the Hopf formula, we avoid the use of grids and present a method that exhibits polynomial scaling in the number of vehicles.