On A Class of Greedy Sparse Recovery Algorithms -- A High Dimensional Approach

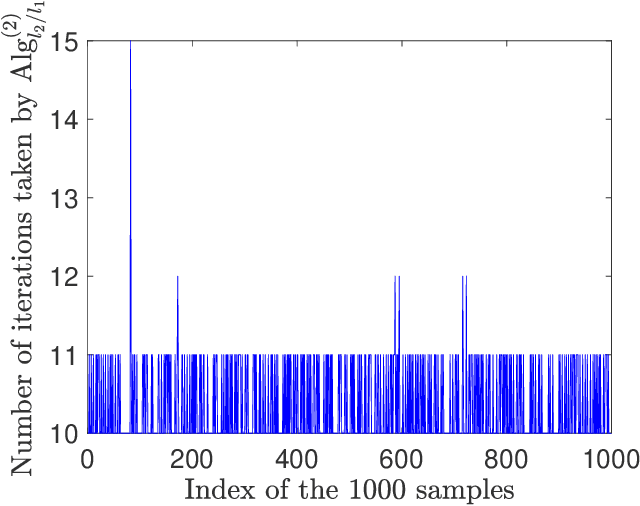
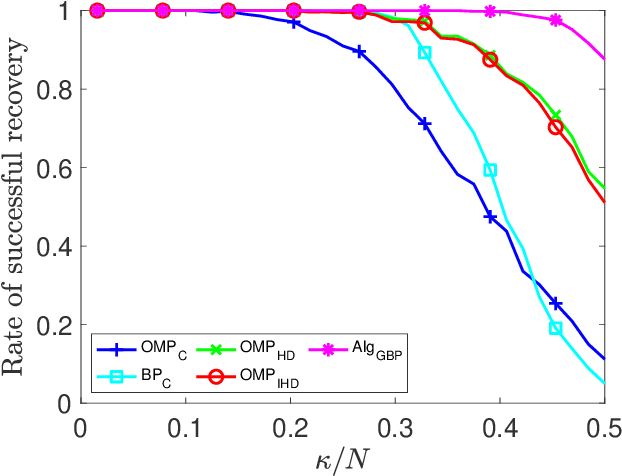
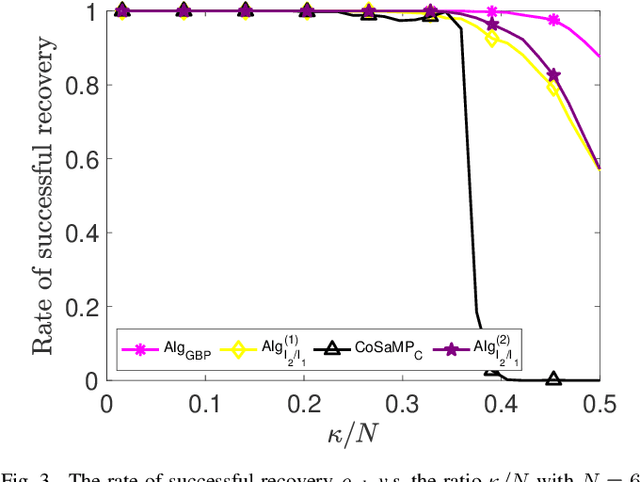
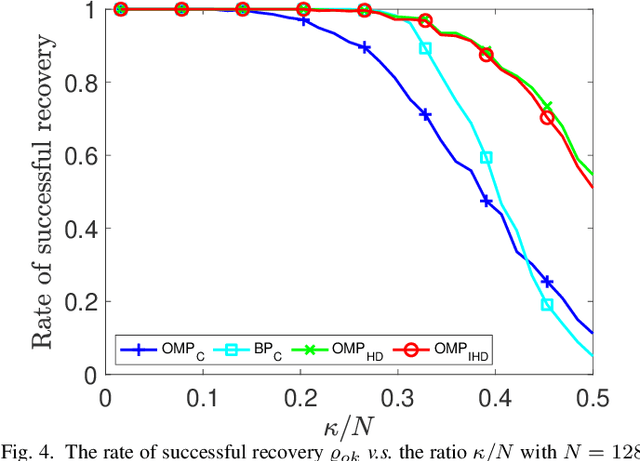
Sparse signal recovery deals with finding the sparest solution of an under-determined linear system $x = Qs$. In this paper, we propose a novel greedy approach to addressing the challenges from such a problem. Such an approach is based on a characterization of solutions to the system, which allows us to work on the sparse recovery in the $s$-space directly with a given measure. With $l_2$-based measure, two OMP-type algorithms are proposed, which significantly outperform the classical OMP algorithm in terms of recovery accuracy while maintaining comparable computational complexity. An $l_1$-based algorithm, denoted as $\text{Alg}_{GBP}$ (greedy basis pursuit) algorithm, is derived. Such an algorithm significantly outperforms the classical BP algorithm. A CoSaMP-type algorithm is also proposed to further enhance the performance of the two proposed OMP-type algorithms. The superior performance of our proposed algorithms is demonstrated through extensive numerical simulations using synthetic data as well as video signals, highlighting their potential for various applications in compressed sensing and signal processing.

A Provable Splitting Approach for Symmetric Nonnegative Matrix Factorization

The symmetric Nonnegative Matrix Factorization (NMF), a special but important class of the general NMF, has found numerous applications in data analysis such as various clustering tasks. Unfortunately, designing fast algorithms for the symmetric NMF is not as easy as for its nonsymmetric counterpart, since the latter admits the splitting property that allows state-of-the-art alternating-type algorithms. To overcome this issue, we first split the decision variable and transform the symmetric NMF to a penalized nonsymmetric one, paving the way for designing efficient alternating-type algorithms. We then show that solving the penalized nonsymmetric reformulation returns a solution to the original symmetric NMF. Moreover, we design a family of alternating-type algorithms and show that they all admit strong convergence guarantee: the generated sequence of iterates is convergent and converges at least sublinearly to a critical point of the original symmetric NMF. Finally, we conduct experiments on both synthetic data and real image clustering to support our theoretical results and demonstrate the performance of the alternating-type algorithms.

Learn to Predict Equilibria via Fixed Point Networks

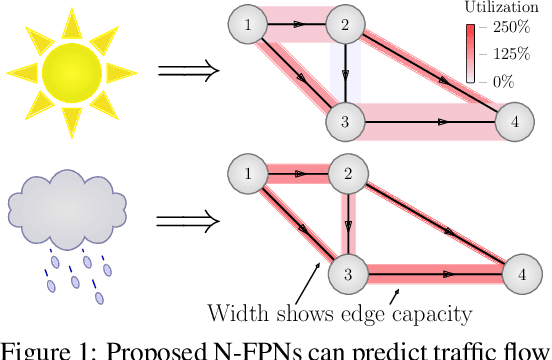
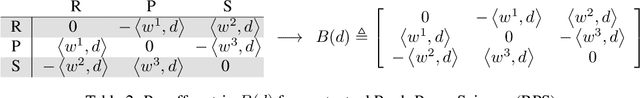
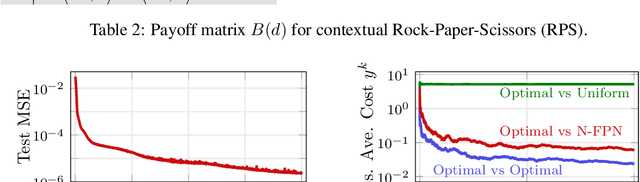
Systems of interacting agents can often be modeled as contextual games, where the context encodes additional information, beyond the control of any agent (e.g. weather for traffic and fiscal policy for market economies). In such systems, the most likely outcome is given by a Nash equilibrium. In many practical settings, only game equilibria are observed, while the optimal parameters for a game model are unknown. This work introduces Nash Fixed Point Networks (N-FPNs), a class of implicit-depth neural networks that output Nash equilibria of contextual games. The N-FPN architecture fuses data-driven modeling with provided constraints. Given equilibrium observations of a contextual game, N-FPN parameters are learnt to predict equilibria outcomes given only the context. We present an end-to-end training scheme for N-FPNs that is simple and memory efficient to implement with existing autodifferentiation tools. N-FPNs also exploit a novel constraint decoupling scheme to avoid costly projections. Provided numerical examples show the efficacy of N-FPNs on atomic and non-atomic games (e.g. traffic routing).

Fixed Point Networks: Implicit Depth Models with Jacobian-Free Backprop

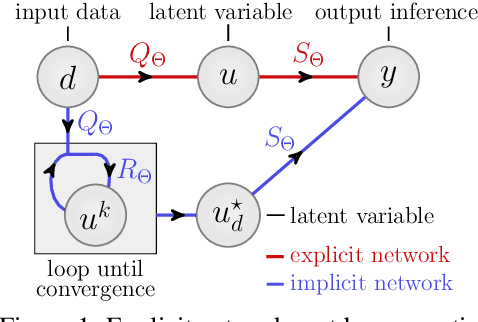
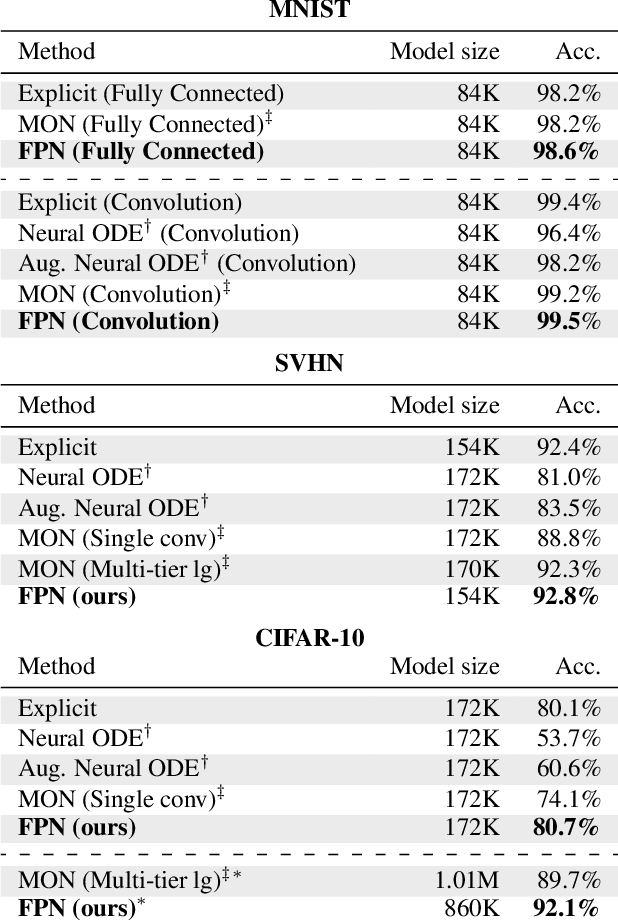
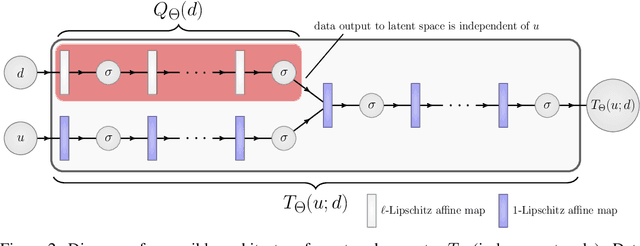
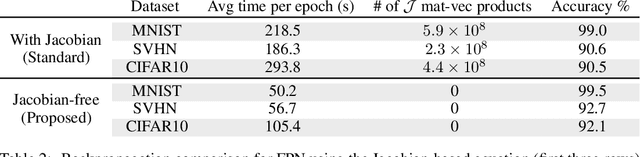
A growing trend in deep learning replaces fixed depth models by approximations of the limit as network depth approaches infinity. This approach uses a portion of network weights to prescribe behavior by defining a limit condition. This makes network depth implicit, varying based on the provided data and an error tolerance. Moreover, existing implicit models can be implemented and trained with fixed memory costs in exchange for additional computational costs. In particular, backpropagation through implicit depth models requires solving a Jacobian-based equation arising from the implicit function theorem. We propose fixed point networks (FPNs), a simple setup for implicit depth learning that guarantees convergence of forward propagation to a unique limit defined by network weights and input data. Our key contribution is to provide a new Jacobian-free backpropagation (JFB) scheme that circumvents the need to solve Jacobian-based equations while maintaining fixed memory costs. This makes FPNs much cheaper to train and easy to implement. Our numerical examples yield state of the art classification results for implicit depth models and outperform corresponding explicit models.

Provable Bregman-divergence based Methods for Nonconvex and Non-Lipschitz Problems

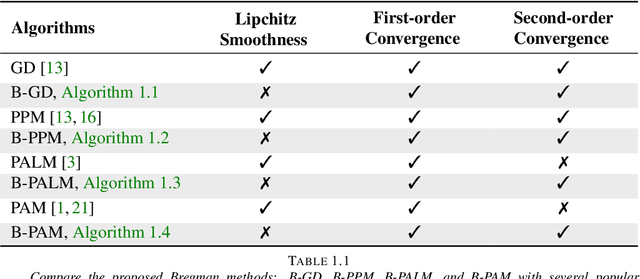
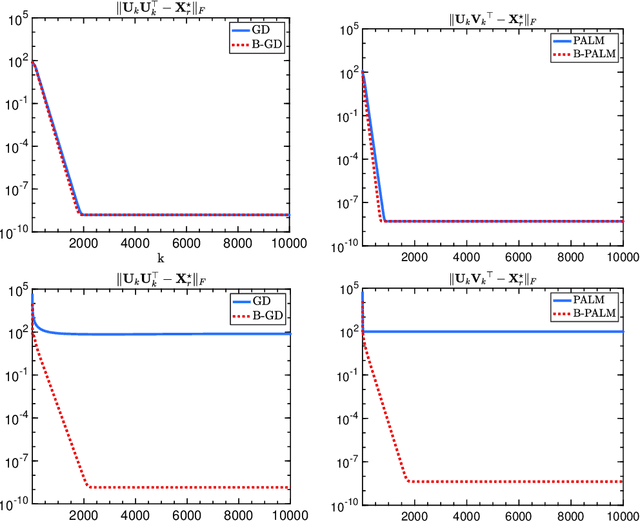
The (global) Lipschitz smoothness condition is crucial in establishing the convergence theory for most optimization methods. Unfortunately, most machine learning and signal processing problems are not Lipschitz smooth. This motivates us to generalize the concept of Lipschitz smoothness condition to the relative smoothness condition, which is satisfied by any finite-order polynomial objective function. Further, this work develops new Bregman-divergence based algorithms that are guaranteed to converge to a second-order stationary point for any relatively smooth problem. In addition, the proposed optimization methods cover both the proximal alternating minimization and the proximal alternating linearized minimization when we specialize the Bregman divergence to the Euclidian distance. Therefore, this work not only develops guaranteed optimization methods for non-Lipschitz smooth problems but also solves an open problem of showing the second-order convergence guarantees for these alternating minimization methods.

Spherical Principal Component Analysis

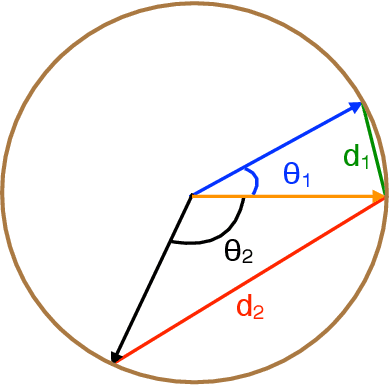
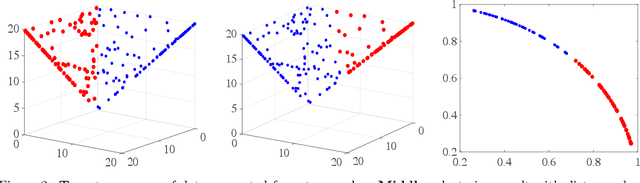
Principal Component Analysis (PCA) is one of the most important methods to handle high dimensional data. However, most of the studies on PCA aim to minimize the loss after projection, which usually measures the Euclidean distance, though in some fields, angle distance is known to be more important and critical for analysis. In this paper, we propose a method by adding constraints on factors to unify the Euclidean distance and angle distance. However, due to the nonconvexity of the objective and constraints, the optimized solution is not easy to obtain. We propose an alternating linearized minimization method to solve it with provable convergence rate and guarantee. Experiments on synthetic data and real-world datasets have validated the effectiveness of our method and demonstrated its advantages over state-of-art clustering methods.

Dropping Symmetry for Fast Symmetric Nonnegative Matrix Factorization

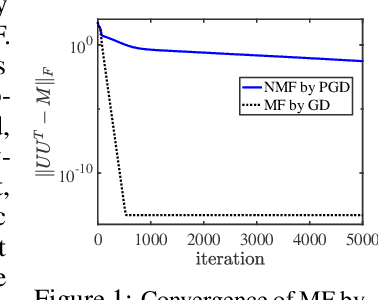
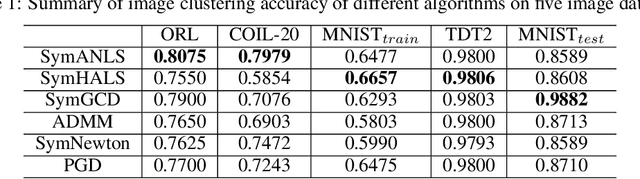
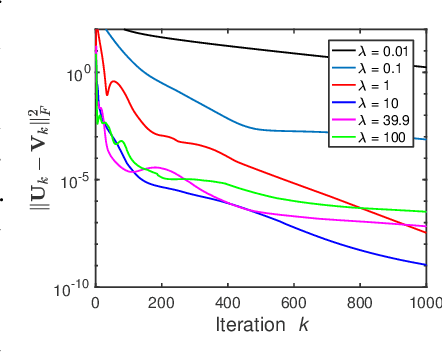
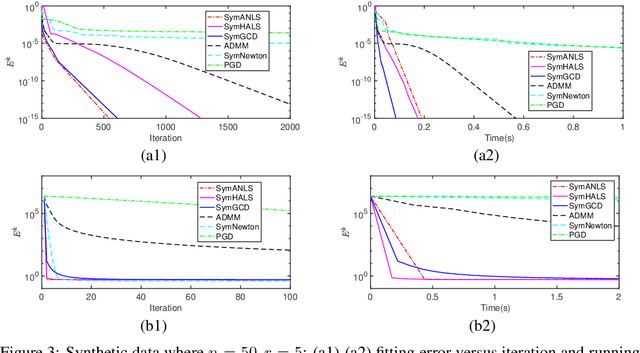
Symmetric nonnegative matrix factorization (NMF), a special but important class of the general NMF, is demonstrated to be useful for data analysis and in particular for various clustering tasks. Unfortunately, designing fast algorithms for Symmetric NMF is not as easy as for the nonsymmetric counterpart, the latter admitting the splitting property that allows efficient alternating-type algorithms. To overcome this issue, we transfer the symmetric NMF to a nonsymmetric one, then we can adopt the idea from the state-of-the-art algorithms for nonsymmetric NMF to design fast algorithms solving symmetric NMF. We rigorously establish that solving nonsymmetric reformulation returns a solution for symmetric NMF and then apply fast alternating based algorithms for the corresponding reformulated problem. Furthermore, we show these fast algorithms admit strong convergence guarantee in the sense that the generated sequence is convergent at least at a sublinear rate and it converges globally to a critical point of the symmetric NMF. We conduct experiments on both synthetic data and image clustering to support our result.

Global Optimality in Distributed Low-rank Matrix Factorization

We study the convergence of a variant of distributed gradient descent (DGD) on a distributed low-rank matrix approximation problem wherein some optimization variables are used for consensus (as in classical DGD) and some optimization variables appear only locally at a single node in the network. We term the resulting algorithm DGD+LOCAL. Using algorithmic connections to gradient descent and geometric connections to the well-behaved landscape of the centralized low-rank matrix approximation problem, we identify sufficient conditions where DGD+LOCAL is guaranteed to converge with exact consensus to a global minimizer of the original centralized problem. For the distributed low-rank matrix approximation problem, these guarantees are stronger---in terms of consensus and optimality---than what appear in the literature for classical DGD and more general problems.

Designing Sparse Sensing Matrices for Image Compression

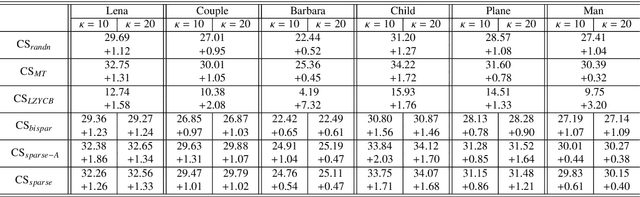
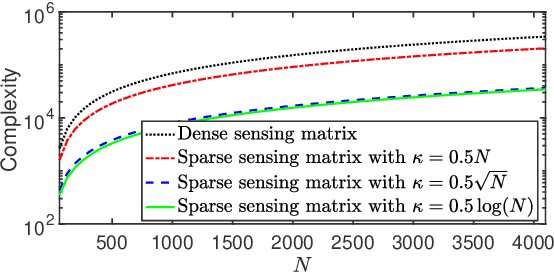
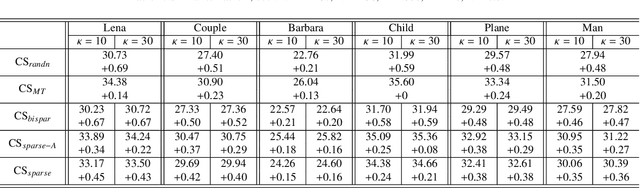
We consider designing a sparse sensing matrix which contains few non-zero entries per row and can be efficiently applied for capturing signals. The optimal sparse sensing matrix is designed so that it is also robust to sparse representation error of the signals and the Gram matrix of the equivalent dictionary is as close as possible to a target Gram matrix with small mutual coherence. An alternating minimization-based algorithm is proposed for solving the optimal design problem. We provide convergence analysis of the proposed algorithm which is proved to have sequence convergence, i.e., it generates a sequence that converges to a stationary point of the minimization problem. Experimental results show that the obtained sparse sensing matrix (even each row is extremely sparse) significantly outperforms a random dense sensing matrix in terms of signal reconstruction accuracy of synthetic data and peak signal-to-noise ratio (PSNR) for real images.

Geometry of Factored Nuclear Norm Regularization

This work investigates the geometry of a nonconvex reformulation of minimizing a general convex loss function $f(X)$ regularized by the matrix nuclear norm $\|X\|_*$. Nuclear-norm regularized matrix inverse problems are at the heart of many applications in machine learning, signal processing, and control. The statistical performance of nuclear norm regularization has been studied extensively in literature using convex analysis techniques. Despite its optimal performance, the resulting optimization has high computational complexity when solved using standard or even tailored fast convex solvers. To develop faster and more scalable algorithms, we follow the proposal of Burer-Monteiro to factor the matrix variable $X$ into the product of two smaller rectangular matrices $X=UV^T$ and also replace the nuclear norm $\|X\|_*$ with $(\|U\|_F^2+\|V\|_F^2)/2$. In spite of the nonconvexity of the factored formulation, we prove that when the convex loss function $f(X)$ is $(2r,4r)$-restricted well-conditioned, each critical point of the factored problem either corresponds to the optimal solution $X^\star$ of the original convex optimization or is a strict saddle point where the Hessian matrix has a strictly negative eigenvalue. Such a geometric structure of the factored formulation allows many local search algorithms to converge to the global optimum with random initializations.