Wu Angela Li
On A Class of Greedy Sparse Recovery Algorithms -- A High Dimensional Approach
Feb 25, 2024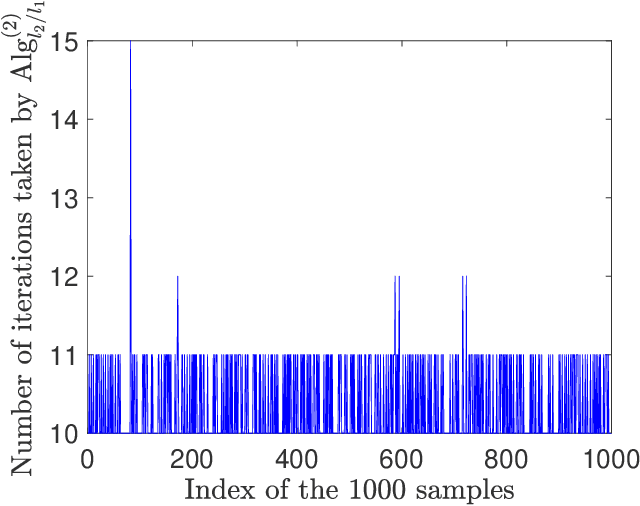
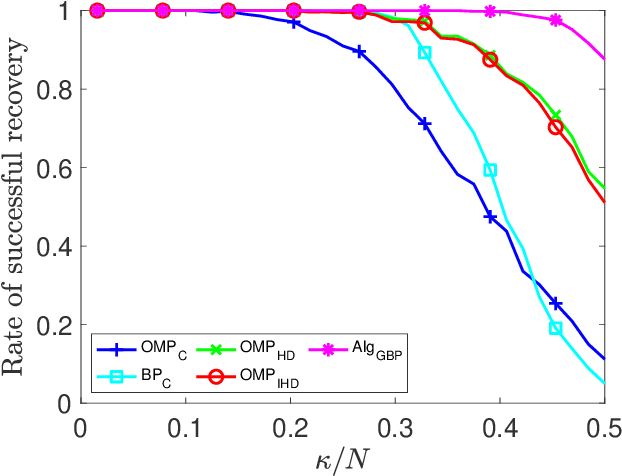
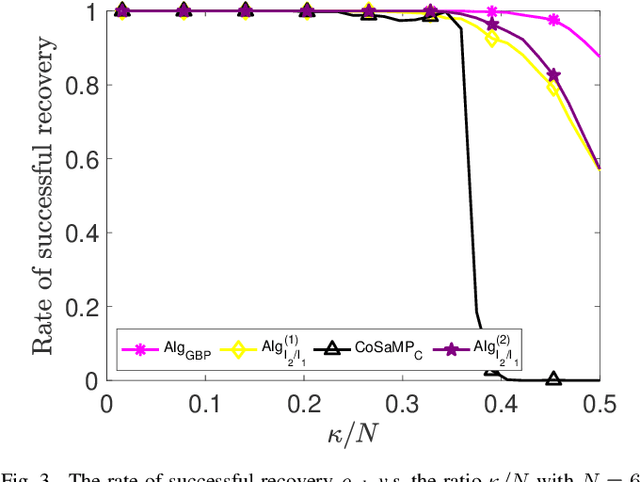
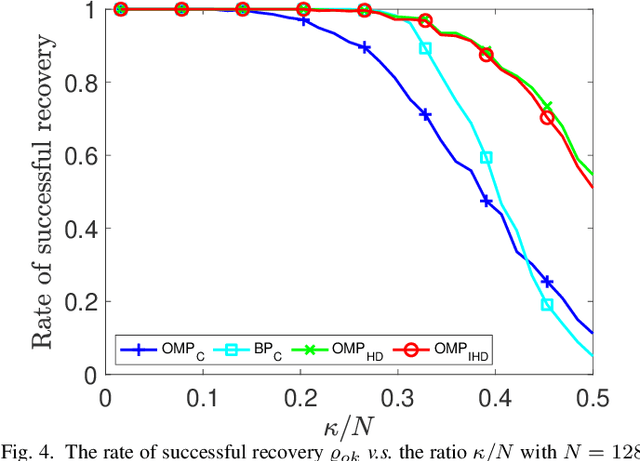
Abstract:Sparse signal recovery deals with finding the sparest solution of an under-determined linear system $x = Qs$. In this paper, we propose a novel greedy approach to addressing the challenges from such a problem. Such an approach is based on a characterization of solutions to the system, which allows us to work on the sparse recovery in the $s$-space directly with a given measure. With $l_2$-based measure, two OMP-type algorithms are proposed, which significantly outperform the classical OMP algorithm in terms of recovery accuracy while maintaining comparable computational complexity. An $l_1$-based algorithm, denoted as $\text{Alg}_{GBP}$ (greedy basis pursuit) algorithm, is derived. Such an algorithm significantly outperforms the classical BP algorithm. A CoSaMP-type algorithm is also proposed to further enhance the performance of the two proposed OMP-type algorithms. The superior performance of our proposed algorithms is demonstrated through extensive numerical simulations using synthetic data as well as video signals, highlighting their potential for various applications in compressed sensing and signal processing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge