Optimal Allocation of Pauli Measurements for Low-rank Quantum State Tomography

The process of reconstructing quantum states from experimental measurements, accomplished through quantum state tomography (QST), plays a crucial role in verifying and benchmarking quantum devices. A key challenge of QST is to find out how the accuracy of the reconstruction depends on the number of state copies used in the measurements. When multiple measurement settings are used, the total number of state copies is determined by multiplying the number of measurement settings with the number of repeated measurements for each setting. Due to statistical noise intrinsic to quantum measurements, a large number of repeated measurements is often used in practice. However, recent studies have shown that even with single-sample measurements--where only one measurement sample is obtained for each measurement setting--high accuracy QST can still be achieved with a sufficiently large number of different measurement settings. In this paper, we establish a theoretical understanding of the trade-off between the number of measurement settings and the number of repeated measurements per setting in QST. Our focus is primarily on low-rank density matrix recovery using Pauli measurements. We delve into the global landscape underlying the low-rank QST problem and demonstrate that the joint consideration of measurement settings and repeated measurements ensures a bounded recovery error for all second-order critical points, to which optimization algorithms tend to converge. This finding suggests the advantage of minimizing the number of repeated measurements per setting when the total number of state copies is held fixed. Additionally, we prove that the Wirtinger gradient descent algorithm can converge to the region of second-order critical points with a linear convergence rate. We have also performed numerical experiments to support our theoretical findings.

Sample-Optimal Quantum State Tomography for Structured Quantum States in One Dimension

Quantum state tomography (QST) remains the gold standard for benchmarking and verifying quantum devices. A recent study has proved that, with Haar random projective measurements, only a $O(n^3)$ number of state copies is required to guarantee bounded recovery error of an matrix product operator (MPO) state of qubits $n$. While this result provides a formal evidence that quantum states with an efficient classical representation can be reconstructed with an efficient number of state copies, the number of state copies required is still significantly larger than the number of independent parameters in the classical representation. In this paper, we attempt to narrow this gap and study whether the number of state copies can saturate the information theoretic bound (i.e., $O(n)$, the number of parameters in the MPOs) using physical quantum measurements. We answer this question affirmatively by using a class of Informationally Complete Positive Operator-Valued Measures (IC-POVMs), including symmetric IC-POVMs (SIC-POVMs) and spherical $t$-designs. For SIC-POVMs and (approximate) spherical 2-designs, we show that the number of state copies to guarantee bounded recovery error of an MPO state with a constrained least-squares estimator depends on the probability distribution of the MPO under the POVM but scales only linearly with $n$ when the distribution is approximately uniform. For spherical $t$-designs with $t\ge3$, we prove that only a number of state copies proportional to the number of independent parameters in the MPO is needed for a guaranteed recovery of any state represented by an MPO. Moreover, we propose a projected gradient descent (PGD) algorithm to solve the constrained least-squares problem and show that it can efficiently find an estimate with bounded recovery error when appropriately initialized.

Non-uniform Array and Frequency Spacing for Regularization-free Gridless DOA

Gridless direction-of-arrival (DOA) estimation with multiple frequencies can be applied in acoustics source localization problems. We formulate this as an atomic norm minimization (ANM) problem and derive an equivalent regularization-free semi-definite program (SDP) thereby avoiding regularization bias. The DOA is retrieved using a Vandermonde decomposition on the Toeplitz matrix obtained from the solution of the SDP. We also propose a fast SDP program to deal with non-uniform array and frequency spacing. For non-uniform spacings, the Toeplitz structure will not exist, but the DOA is retrieved via irregular Vandermonde decomposition (IVD), and we theoretically guarantee the existence of the IVD. We extend ANM to the multiple measurement vector (MMV) cases and derive its equivalent regularization-free SDP. Using multiple frequencies and the MMV model, we can resolve more sources than the number of physical sensors for a uniform linear array. Numerical results demonstrate that the regularization-free framework is robust to noise and aliasing, and it overcomes the regularization bias.

Guaranteed Nonconvex Factorization Approach for Tensor Train Recovery

In this paper, we provide the first convergence guarantee for the factorization approach. Specifically, to avoid the scaling ambiguity and to facilitate theoretical analysis, we optimize over the so-called left-orthogonal TT format which enforces orthonormality among most of the factors. To ensure the orthonormal structure, we utilize the Riemannian gradient descent (RGD) for optimizing those factors over the Stiefel manifold. We first delve into the TT factorization problem and establish the local linear convergence of RGD. Notably, the rate of convergence only experiences a linear decline as the tensor order increases. We then study the sensing problem that aims to recover a TT format tensor from linear measurements. Assuming the sensing operator satisfies the restricted isometry property (RIP), we show that with a proper initialization, which could be obtained through spectral initialization, RGD also converges to the ground-truth tensor at a linear rate. Furthermore, we expand our analysis to encompass scenarios involving Gaussian noise in the measurements. We prove that RGD can reliably recover the ground truth at a linear rate, with the recovery error exhibiting only polynomial growth in relation to the tensor order. We conduct various experiments to validate our theoretical findings.

Stable Tomography for Structured Quantum States

The reconstruction of quantum states from experimental measurements, often achieved using quantum state tomography (QST), is crucial for the verification and benchmarking of quantum devices. However, performing QST for a generic unstructured quantum state requires an enormous number of state copies that grows \emph{exponentially} with the number of individual quanta in the system, even for the most optimal measurement settings. Fortunately, many physical quantum states, such as states generated by noisy, intermediate-scale quantum computers, are usually structured. In one dimension, such states are expected to be well approximated by matrix product operators (MPOs) with a finite matrix/bond dimension independent of the number of qubits, therefore enabling efficient state representation. Nevertheless, it is still unclear whether efficient QST can be performed for these states in general. In this paper, we attempt to bridge this gap and establish theoretical guarantees for the stable recovery of MPOs using tools from compressive sensing and the theory of empirical processes. We begin by studying two types of random measurement settings: Gaussian measurements and Haar random rank-one Positive Operator Valued Measures (POVMs). We show that the information contained in an MPO with a finite bond dimension can be preserved using a number of random measurements that depends only \emph{linearly} on the number of qubits, assuming no statistical error of the measurements. We then study MPO-based QST with physical quantum measurements through Haar random rank-one POVMs that can be implemented on quantum computers. We prove that only a \emph{polynomial} number of state copies in the number of qubits is required to guarantee bounded recovery error of an MPO state.

Gridless DOA Estimation with Multiple Frequencies

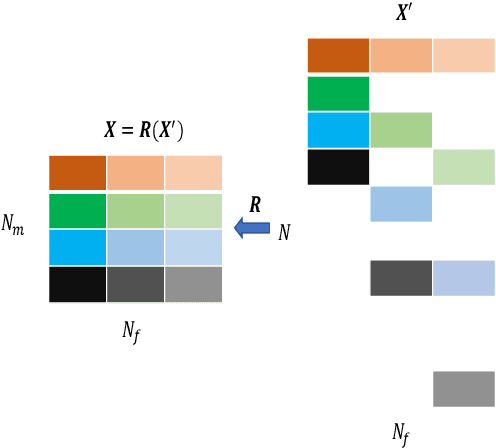
Direction-of-arrival (DOA) estimation is widely applied in acoustic source localization. A multi-frequency model is suitable for characterizing the broadband structure in acoustic signals. In this paper, the continuous (gridless) DOA estimation problem with multiple frequencies is considered. This problem is formulated as an atomic norm minimization (ANM) problem. The ANM problem is equivalent to a semi-definite program (SDP) which can be solved by an off-the-shelf SDP solver. The dual certificate condition is provided to certify the optimality of the SDP solution so that the sources can be localized by finding the roots of a polynomial. We also construct the dual polynomial to satisfy the dual certificate condition and show that such a construction exists when the source amplitude has a uniform magnitude. In multi-frequency ANM, spatial aliasing of DOAs at higher frequencies can cause challenges. We discuss this issue extensively and propose a robust solution to combat aliasing. Numerical results support our theoretical findings and demonstrate the effectiveness of the proposed method.

Error Analysis of Tensor-Train Cross Approximation

Tensor train decomposition is widely used in machine learning and quantum physics due to its concise representation of high-dimensional tensors, overcoming the curse of dimensionality. Cross approximation-originally developed for representing a matrix from a set of selected rows and columns-is an efficient method for constructing a tensor train decomposition of a tensor from few of its entries. While tensor train cross approximation has achieved remarkable performance in practical applications, its theoretical analysis, in particular regarding the error of the approximation, is so far lacking. To our knowledge, existing results only provide element-wise approximation accuracy guarantees, which lead to a very loose bound when extended to the entire tensor. In this paper, we bridge this gap by providing accuracy guarantees in terms of the entire tensor for both exact and noisy measurements. Our results illustrate how the choice of selected subtensors affects the quality of the cross approximation and that the approximation error caused by model error and/or measurement error may not grow exponentially with the order of the tensor. These results are verified by numerical experiments, and may have important implications for the usefulness of cross approximations for high-order tensors, such as those encountered in the description of quantum many-body states.

On Grid Compressive Sensing for Spherical Field Measurements in Acoustics

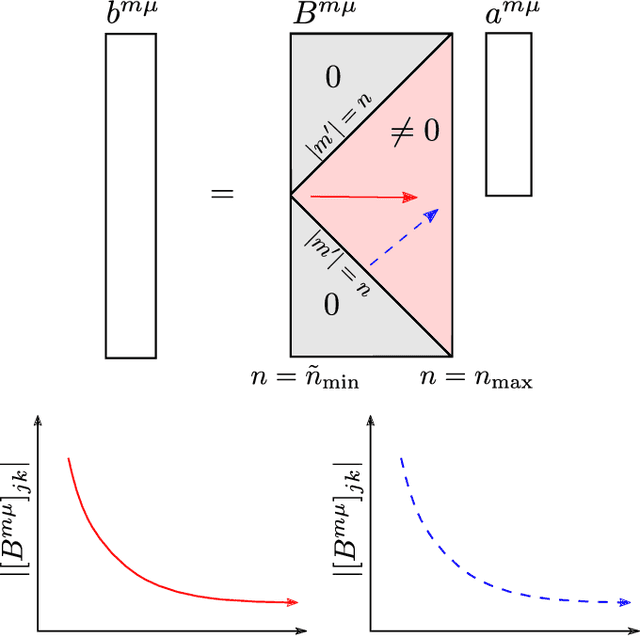
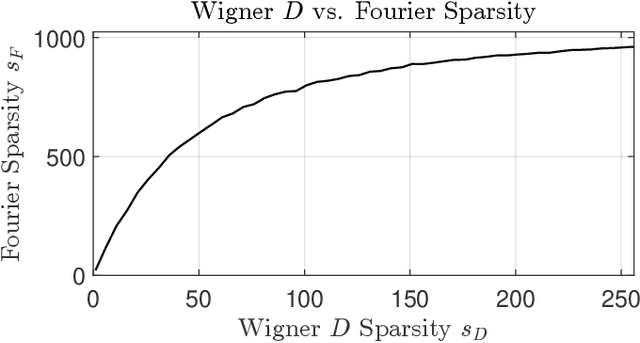
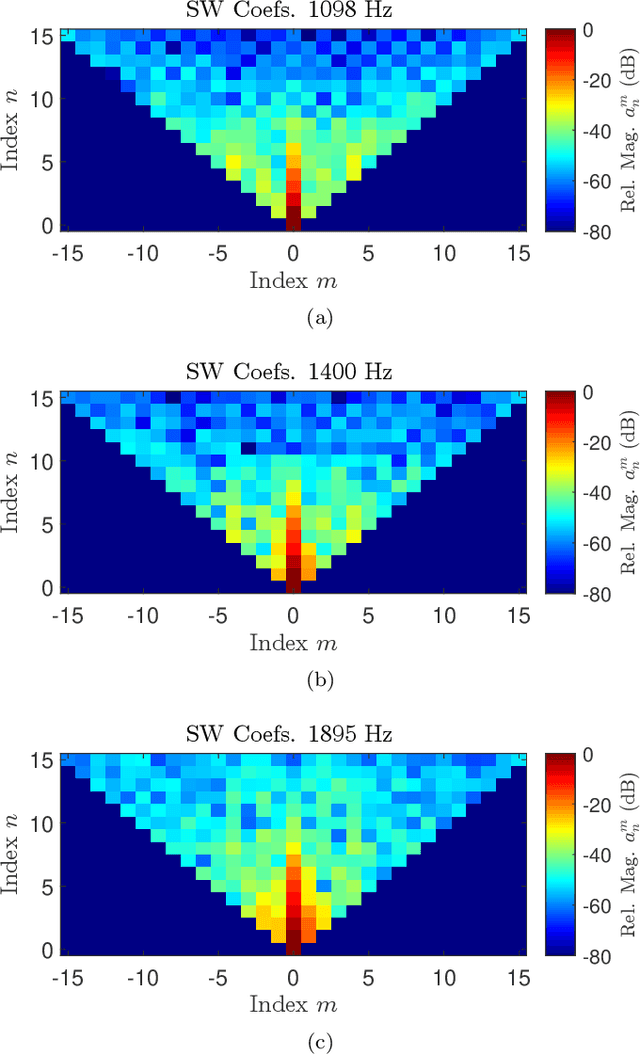
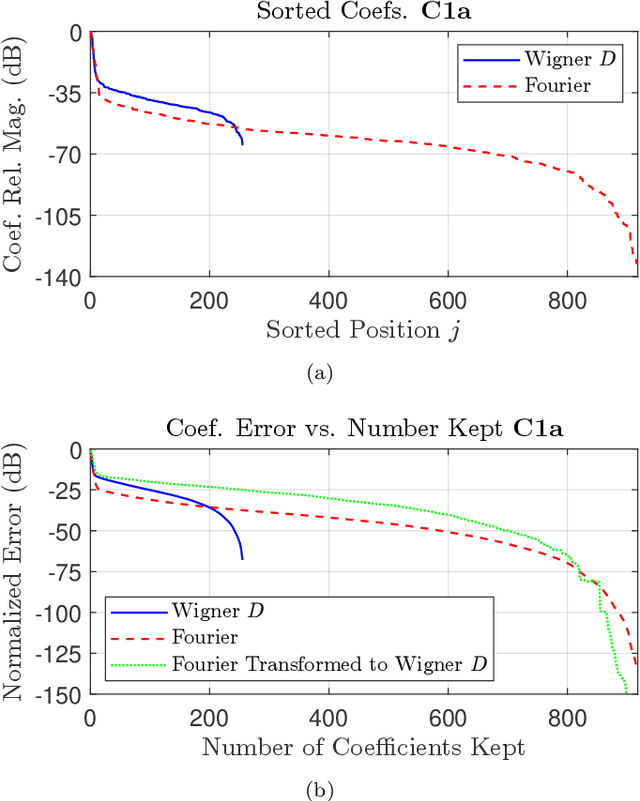
We derive a theoretically guaranteed compressive sensing method for acoustic field reconstructions using spherical field measurements on a predefined grid. This method can be used to reconstruct sparse band-limited spherical harmonic or Wigner $D$-function series. Contrasting typical compressive sensing methods for spherical harmonic or Wigner $D$-function series that use random measurements on the sphere or rotation group, the new method samples on an equiangular grid in those domains, which is a commonly used sampling pattern. Using the periodic extension of the Wigner $D$-functions, we transform the reconstruction of a Wigner $D$-function series (of which spherical harmonics are a special case) into a multi-dimensional Fourier domain reconstruction problem. We establish that this transformation maintains sparsity in cases of interest and provide numerical studies of the transformation's effect on sparsity. We also provide numerical studies of the reconstruction performance of the compressive sensing approach compared to classical Nyquist sampling. In the cases tested, we find accurate compressive sensing reconstructions need only a fraction of the measurements dictated by the Nyquist sampling theorem. Moreover, using one-third of the measurements or less, the compressive sensing method can provide over 20 dB more denoising capabilities than oversampling with classical Fourier theory.

Restricted Domain Compressive Sensing for Antenna Metrology

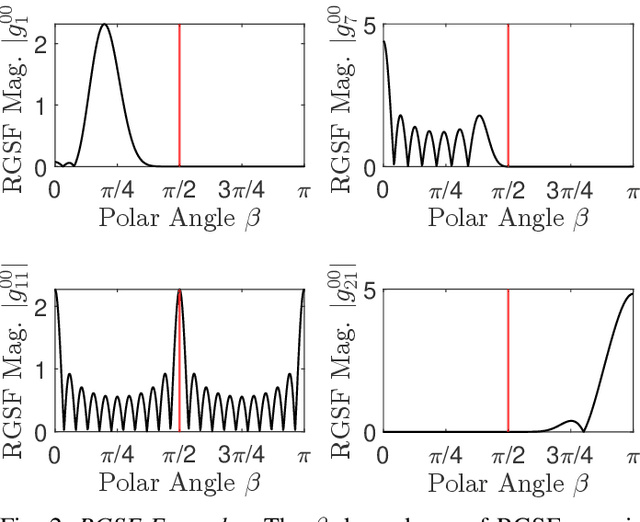
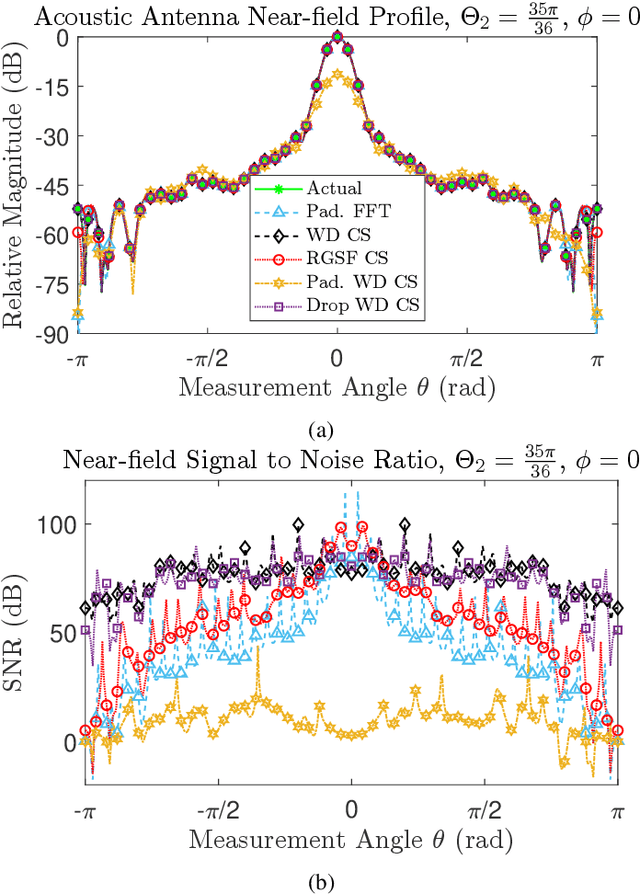
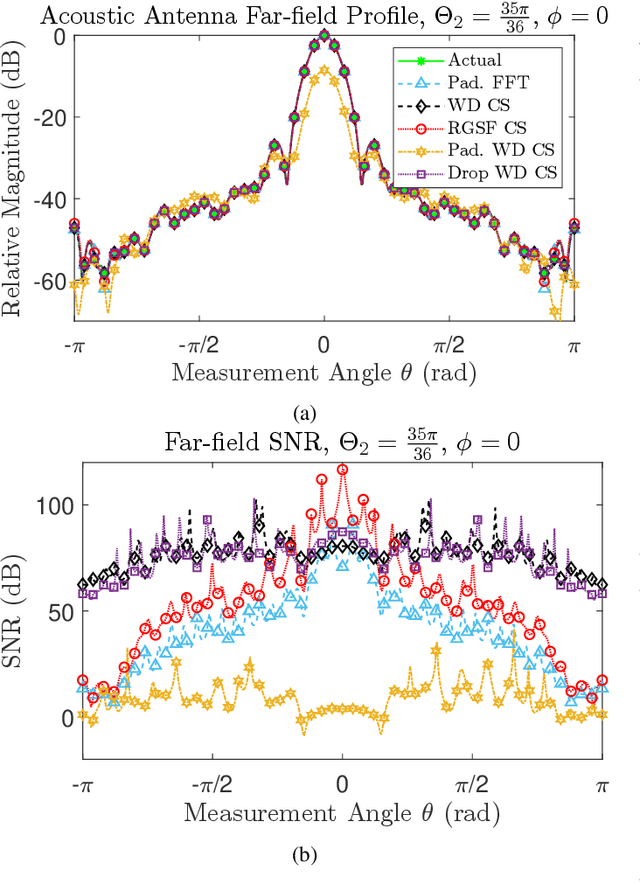
In this paper, we prove a compressive sensing guarantee for restricted measurement domains in spherical near-field to far-field transformations for antenna metrology. We do so by first defining Slepian functions on a measurement sub-domain $R$ of the rotation group $\mathrm{SO}(3)$, the full domain of the linear inverse problem associated with spherical near-field to far-field transformations. Then, we transform the inverse problem from the measurement basis, the bounded orthonormal system of band-limited Wigner $D$-functions on $\mathrm{SO}(3)$, to the Slepian functions in a way that preserves sparsity. Contrasting methods using Wigner $D$-functions that require measurements on all of $\mathrm{SO}(3)$, we show that the orthogonality structure of the Slepian functions only requires measurements on the sub-domain $R$, which is select-able. Due to the particulars of this approach and the inherent presence of Slepian functions with low concentrations on $R$, our approach gives the highest accuracy when the signal under study is well concentrated on $R$. We provide numerical examples of our method in comparison with other classical and compressive sensing approaches. In terms of reconstruction quality, we find that our method outperforms the other compressive sensing approaches we test and is at least as good as classical approaches but with a significant reduction in the number of measurements.

Digital Beamforming Robust to Time-Varying Carrier Frequency Offset

Adaptive interference cancellation is rapidly becoming a necessity for our modern wireless communication systems, due to the proliferation of wireless devices that interfere with each other. To cancel interference, digital beamforming algorithms adaptively adjust the weight vector of the antenna array, and in turn its radiation pattern, to minimize interference while maximizing the desired signal power. While these algorithms are effective in ideal scenarios, they are sensitive to signal corruptions. In this work, we consider the case when the transmitter and receiver in a communication system cannot be synchronized, resulting in a carrier frequency offset that corrupts the signal. We present novel beamforming algorithms that are robust to signal corruptions arising from this time-variant carrier frequency offset. In particular, we bring in the Discrete Prolate Spheroidal Sequences (DPSS's) and propose two atomic-norm-minimization (ANM)-based methods in both 1D and 2D frameworks to design a weight vector that can be used to cancel interference when there exist unknown time-varying frequency drift in the pilot and interferer signals. Both algorithms do not assume a pilot signal is known. Noting that solving ANM optimization problems via semi-definite programs can be a computational burden, we also present a novel fast algorithm to approximately solve our 1D ANM optimization problem. Finally, we confirm the benefits of our proposed algorithms and show the advantages over existing approaches with a series of experiments.