Error Analysis of Tensor-Train Cross Approximation
Paper and Code
Jul 09, 2022
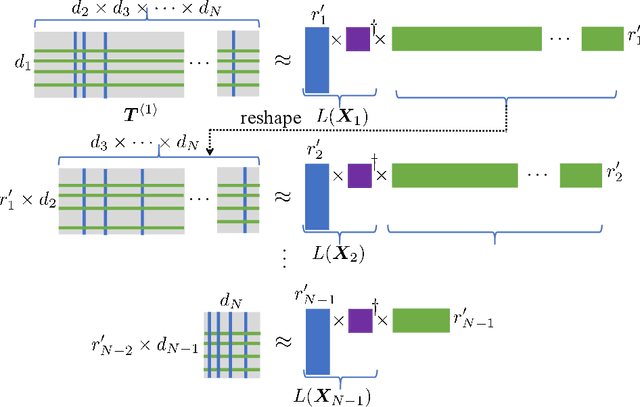
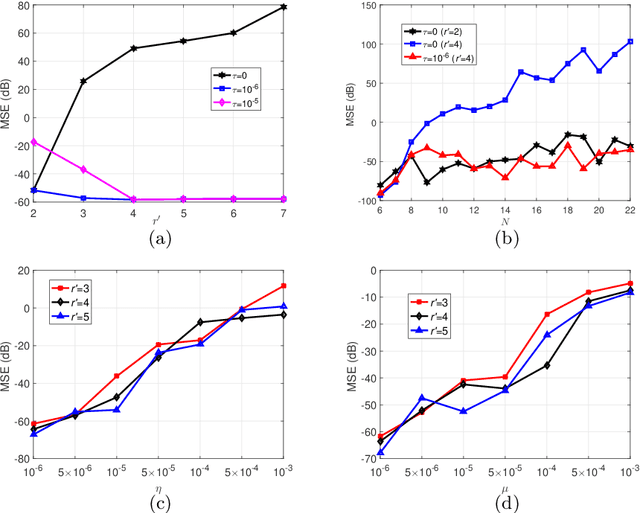

Tensor train decomposition is widely used in machine learning and quantum physics due to its concise representation of high-dimensional tensors, overcoming the curse of dimensionality. Cross approximation-originally developed for representing a matrix from a set of selected rows and columns-is an efficient method for constructing a tensor train decomposition of a tensor from few of its entries. While tensor train cross approximation has achieved remarkable performance in practical applications, its theoretical analysis, in particular regarding the error of the approximation, is so far lacking. To our knowledge, existing results only provide element-wise approximation accuracy guarantees, which lead to a very loose bound when extended to the entire tensor. In this paper, we bridge this gap by providing accuracy guarantees in terms of the entire tensor for both exact and noisy measurements. Our results illustrate how the choice of selected subtensors affects the quality of the cross approximation and that the approximation error caused by model error and/or measurement error may not grow exponentially with the order of the tensor. These results are verified by numerical experiments, and may have important implications for the usefulness of cross approximations for high-order tensors, such as those encountered in the description of quantum many-body states.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge