Error Analysis of Tensor-Train Cross Approximation

Tensor train decomposition is widely used in machine learning and quantum physics due to its concise representation of high-dimensional tensors, overcoming the curse of dimensionality. Cross approximation-originally developed for representing a matrix from a set of selected rows and columns-is an efficient method for constructing a tensor train decomposition of a tensor from few of its entries. While tensor train cross approximation has achieved remarkable performance in practical applications, its theoretical analysis, in particular regarding the error of the approximation, is so far lacking. To our knowledge, existing results only provide element-wise approximation accuracy guarantees, which lead to a very loose bound when extended to the entire tensor. In this paper, we bridge this gap by providing accuracy guarantees in terms of the entire tensor for both exact and noisy measurements. Our results illustrate how the choice of selected subtensors affects the quality of the cross approximation and that the approximation error caused by model error and/or measurement error may not grow exponentially with the order of the tensor. These results are verified by numerical experiments, and may have important implications for the usefulness of cross approximations for high-order tensors, such as those encountered in the description of quantum many-body states.

Unsupervised machine learning of quantum phase transitions using diffusion maps

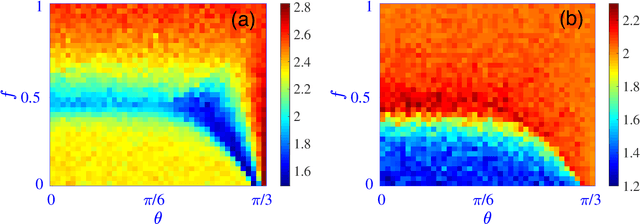
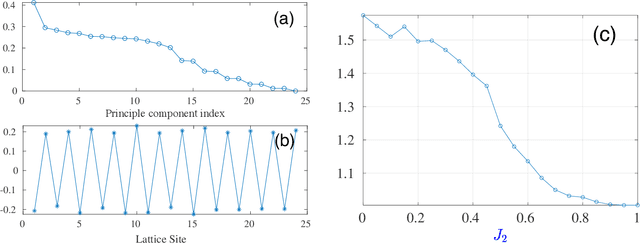
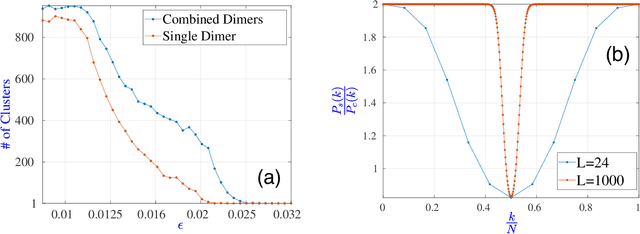
Experimental quantum simulators have become large and complex enough that discovering new physics from the huge amount of measurement data can be quite challenging, especially when little theoretical understanding of the simulated model is available. Unsupervised machine learning methods are particularly promising in overcoming this challenge. For the specific task of learning quantum phase transitions, unsupervised machine learning methods have primarily been developed for phase transitions characterized by simple order parameters, typically linear in the measured observables. However, such methods often fail for more complicated phase transitions, such as those involving incommensurate phases, valence-bond solids, topological order, and many-body localization. We show that the diffusion map method, which performs nonlinear dimensionality reduction and spectral clustering of the measurement data, has significant potential for learning such complex phase transitions unsupervised. This method works for measurements of local observables in a single basis and is thus readily applicable to many experimental quantum simulators as a versatile tool for learning various quantum phases and phase transitions.