Optimal Allocation of Pauli Measurements for Low-rank Quantum State Tomography

The process of reconstructing quantum states from experimental measurements, accomplished through quantum state tomography (QST), plays a crucial role in verifying and benchmarking quantum devices. A key challenge of QST is to find out how the accuracy of the reconstruction depends on the number of state copies used in the measurements. When multiple measurement settings are used, the total number of state copies is determined by multiplying the number of measurement settings with the number of repeated measurements for each setting. Due to statistical noise intrinsic to quantum measurements, a large number of repeated measurements is often used in practice. However, recent studies have shown that even with single-sample measurements--where only one measurement sample is obtained for each measurement setting--high accuracy QST can still be achieved with a sufficiently large number of different measurement settings. In this paper, we establish a theoretical understanding of the trade-off between the number of measurement settings and the number of repeated measurements per setting in QST. Our focus is primarily on low-rank density matrix recovery using Pauli measurements. We delve into the global landscape underlying the low-rank QST problem and demonstrate that the joint consideration of measurement settings and repeated measurements ensures a bounded recovery error for all second-order critical points, to which optimization algorithms tend to converge. This finding suggests the advantage of minimizing the number of repeated measurements per setting when the total number of state copies is held fixed. Additionally, we prove that the Wirtinger gradient descent algorithm can converge to the region of second-order critical points with a linear convergence rate. We have also performed numerical experiments to support our theoretical findings.

Sample-Optimal Quantum State Tomography for Structured Quantum States in One Dimension

Quantum state tomography (QST) remains the gold standard for benchmarking and verifying quantum devices. A recent study has proved that, with Haar random projective measurements, only a $O(n^3)$ number of state copies is required to guarantee bounded recovery error of an matrix product operator (MPO) state of qubits $n$. While this result provides a formal evidence that quantum states with an efficient classical representation can be reconstructed with an efficient number of state copies, the number of state copies required is still significantly larger than the number of independent parameters in the classical representation. In this paper, we attempt to narrow this gap and study whether the number of state copies can saturate the information theoretic bound (i.e., $O(n)$, the number of parameters in the MPOs) using physical quantum measurements. We answer this question affirmatively by using a class of Informationally Complete Positive Operator-Valued Measures (IC-POVMs), including symmetric IC-POVMs (SIC-POVMs) and spherical $t$-designs. For SIC-POVMs and (approximate) spherical 2-designs, we show that the number of state copies to guarantee bounded recovery error of an MPO state with a constrained least-squares estimator depends on the probability distribution of the MPO under the POVM but scales only linearly with $n$ when the distribution is approximately uniform. For spherical $t$-designs with $t\ge3$, we prove that only a number of state copies proportional to the number of independent parameters in the MPO is needed for a guaranteed recovery of any state represented by an MPO. Moreover, we propose a projected gradient descent (PGD) algorithm to solve the constrained least-squares problem and show that it can efficiently find an estimate with bounded recovery error when appropriately initialized.

Stable Tomography for Structured Quantum States

The reconstruction of quantum states from experimental measurements, often achieved using quantum state tomography (QST), is crucial for the verification and benchmarking of quantum devices. However, performing QST for a generic unstructured quantum state requires an enormous number of state copies that grows \emph{exponentially} with the number of individual quanta in the system, even for the most optimal measurement settings. Fortunately, many physical quantum states, such as states generated by noisy, intermediate-scale quantum computers, are usually structured. In one dimension, such states are expected to be well approximated by matrix product operators (MPOs) with a finite matrix/bond dimension independent of the number of qubits, therefore enabling efficient state representation. Nevertheless, it is still unclear whether efficient QST can be performed for these states in general. In this paper, we attempt to bridge this gap and establish theoretical guarantees for the stable recovery of MPOs using tools from compressive sensing and the theory of empirical processes. We begin by studying two types of random measurement settings: Gaussian measurements and Haar random rank-one Positive Operator Valued Measures (POVMs). We show that the information contained in an MPO with a finite bond dimension can be preserved using a number of random measurements that depends only \emph{linearly} on the number of qubits, assuming no statistical error of the measurements. We then study MPO-based QST with physical quantum measurements through Haar random rank-one POVMs that can be implemented on quantum computers. We prove that only a \emph{polynomial} number of state copies in the number of qubits is required to guarantee bounded recovery error of an MPO state.

Error Analysis of Tensor-Train Cross Approximation

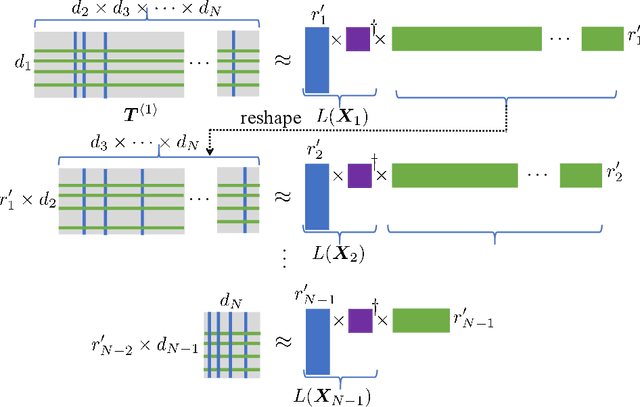
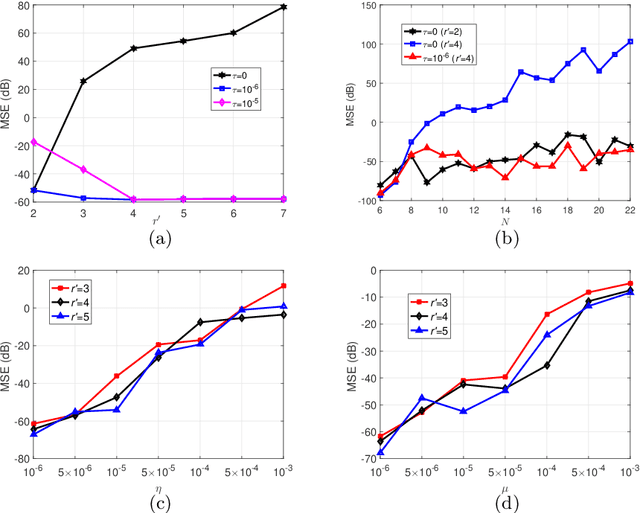
Tensor train decomposition is widely used in machine learning and quantum physics due to its concise representation of high-dimensional tensors, overcoming the curse of dimensionality. Cross approximation-originally developed for representing a matrix from a set of selected rows and columns-is an efficient method for constructing a tensor train decomposition of a tensor from few of its entries. While tensor train cross approximation has achieved remarkable performance in practical applications, its theoretical analysis, in particular regarding the error of the approximation, is so far lacking. To our knowledge, existing results only provide element-wise approximation accuracy guarantees, which lead to a very loose bound when extended to the entire tensor. In this paper, we bridge this gap by providing accuracy guarantees in terms of the entire tensor for both exact and noisy measurements. Our results illustrate how the choice of selected subtensors affects the quality of the cross approximation and that the approximation error caused by model error and/or measurement error may not grow exponentially with the order of the tensor. These results are verified by numerical experiments, and may have important implications for the usefulness of cross approximations for high-order tensors, such as those encountered in the description of quantum many-body states.

Unsupervised machine learning of quantum phase transitions using diffusion maps

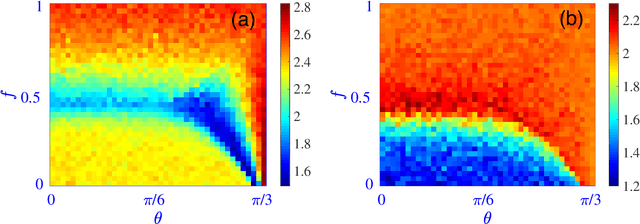
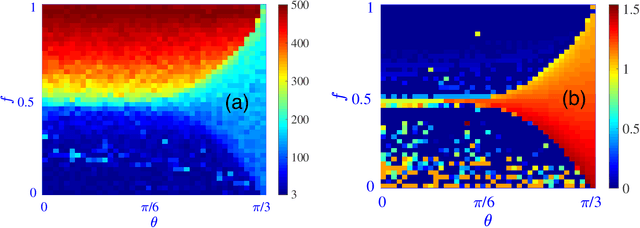
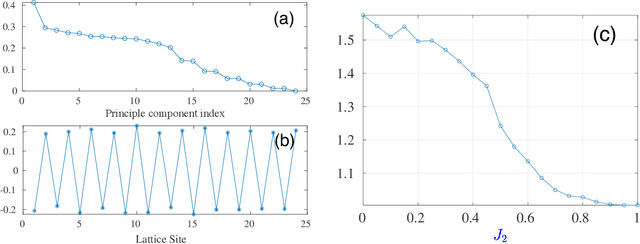
Experimental quantum simulators have become large and complex enough that discovering new physics from the huge amount of measurement data can be quite challenging, especially when little theoretical understanding of the simulated model is available. Unsupervised machine learning methods are particularly promising in overcoming this challenge. For the specific task of learning quantum phase transitions, unsupervised machine learning methods have primarily been developed for phase transitions characterized by simple order parameters, typically linear in the measured observables. However, such methods often fail for more complicated phase transitions, such as those involving incommensurate phases, valence-bond solids, topological order, and many-body localization. We show that the diffusion map method, which performs nonlinear dimensionality reduction and spectral clustering of the measurement data, has significant potential for learning such complex phase transitions unsupervised. This method works for measurements of local observables in a single basis and is thus readily applicable to many experimental quantum simulators as a versatile tool for learning various quantum phases and phase transitions.