Differentiable physics for sound field reconstruction

Sound field reconstruction involves estimating sound fields from a limited number of spatially distributed observations. This work introduces a differentiable physics approach for sound field reconstruction, where the initial conditions of the wave equation are approximated with a neural network, and the differential operator is computed with a differentiable numerical solver. The use of a numerical solver enables a stable network training while enforcing the physics as a strong constraint, in contrast to conventional physics-informed neural networks, which include the physics as a constraint in the loss function. We introduce an additional sparsity-promoting constraint to achieve meaningful solutions even under severe undersampling conditions. Experiments demonstrate that the proposed approach can reconstruct sound fields under extreme data scarcity, achieving higher accuracy and better convergence compared to physics-informed neural networks.

Real, Fake, or Manipulated? Detecting Machine-Influenced Text

Large Language Model (LLMs) can be used to write or modify documents, presenting a challenge for understanding the intent behind their use. For example, benign uses may involve using LLM on a human-written document to improve its grammar or to translate it into another language. However, a document entirely produced by a LLM may be more likely to be used to spread misinformation than simple translation (\eg, from use by malicious actors or simply by hallucinating). Prior works in Machine Generated Text (MGT) detection mostly focus on simply identifying whether a document was human or machine written, ignoring these fine-grained uses. In this paper, we introduce a HiErarchical, length-RObust machine-influenced text detector (HERO), which learns to separate text samples of varying lengths from four primary types: human-written, machine-generated, machine-polished, and machine-translated. HERO accomplishes this by combining predictions from length-specialist models that have been trained with Subcategory Guidance. Specifically, for categories that are easily confused (\eg, different source languages), our Subcategory Guidance module encourages separation of the fine-grained categories, boosting performance. Extensive experiments across five LLMs and six domains demonstrate the benefits of our HERO, outperforming the state-of-the-art by 2.5-3 mAP on average.

Scaling Continuous Kernels with Sparse Fourier Domain Learning

We address three key challenges in learning continuous kernel representations: computational efficiency, parameter efficiency, and spectral bias. Continuous kernels have shown significant potential, but their practical adoption is often limited by high computational and memory demands. Additionally, these methods are prone to spectral bias, which impedes their ability to capture high-frequency details. To overcome these limitations, we propose a novel approach that leverages sparse learning in the Fourier domain. Our method enables the efficient scaling of continuous kernels, drastically reduces computational and memory requirements, and mitigates spectral bias by exploiting the Gibbs phenomenon.

Efficient Sound Field Reconstruction with Conditional Invertible Neural Networks

In this study, we introduce a method for estimating sound fields in reverberant environments using a conditional invertible neural network (CINN). Sound field reconstruction can be hindered by experimental errors, limited spatial data, model mismatches, and long inference times, leading to potentially flawed and prolonged characterizations. Further, the complexity of managing inherent uncertainties often escalates computational demands or is neglected in models. Our approach seeks to balance accuracy and computational efficiency, while incorporating uncertainty estimates to tailor reconstructions to specific needs. By training a CINN with Monte Carlo simulations of random wave fields, our method reduces the dependency on extensive datasets and enables inference from sparse experimental data. The CINN proves versatile at reconstructing Room Impulse Responses (RIRs), by acting either as a likelihood model for maximum a posteriori estimation or as an approximate posterior distribution through amortized Bayesian inference. Compared to traditional Bayesian methods, the CINN achieves similar accuracy with greater efficiency and without requiring its adaptation to distinct sound field conditions.

Non-uniform Array and Frequency Spacing for Regularization-free Gridless DOA

Gridless direction-of-arrival (DOA) estimation with multiple frequencies can be applied in acoustics source localization problems. We formulate this as an atomic norm minimization (ANM) problem and derive an equivalent regularization-free semi-definite program (SDP) thereby avoiding regularization bias. The DOA is retrieved using a Vandermonde decomposition on the Toeplitz matrix obtained from the solution of the SDP. We also propose a fast SDP program to deal with non-uniform array and frequency spacing. For non-uniform spacings, the Toeplitz structure will not exist, but the DOA is retrieved via irregular Vandermonde decomposition (IVD), and we theoretically guarantee the existence of the IVD. We extend ANM to the multiple measurement vector (MMV) cases and derive its equivalent regularization-free SDP. Using multiple frequencies and the MMV model, we can resolve more sources than the number of physical sensors for a uniform linear array. Numerical results demonstrate that the regularization-free framework is robust to noise and aliasing, and it overcomes the regularization bias.

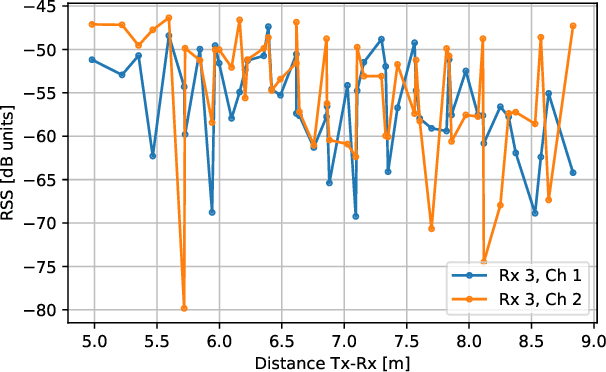
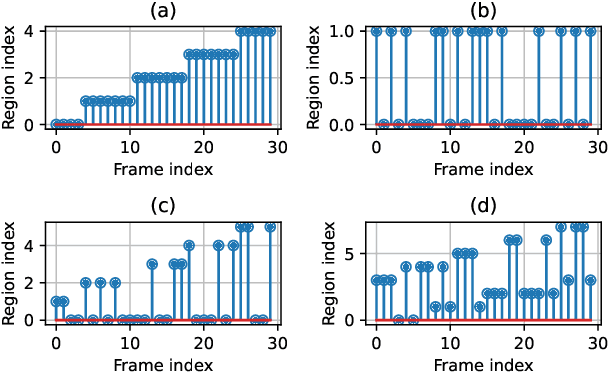
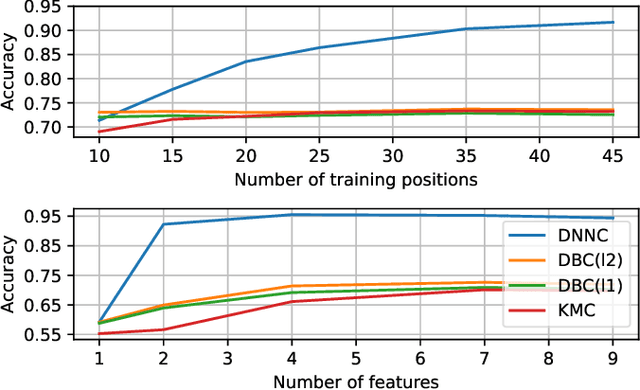
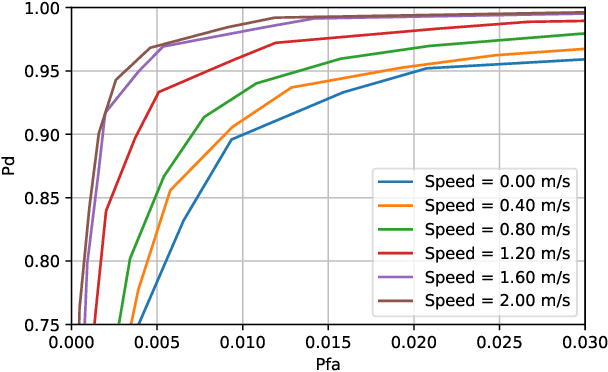
Spoofing Attack Detection in the Physical Layer with Robustness to User Movement

In a spoofing attack, an attacker impersonates a legitimate user to access or modify data belonging to the latter. Typical approaches for spoofing detection in the physical layer declare an attack when a change is observed in certain channel features, such as the received signal strength (RSS) measured by spatially distributed receivers. However, since channels change over time, for example due to user movement, such approaches are impractical. To sidestep this limitation, this paper proposes a scheme that combines the decisions of a position-change detector based on a deep neural network to distinguish spoofing from movement. Building upon community detection on graphs, the sequence of received frames is partitioned into subsequences to detect concurrent transmissions from distinct locations. The scheme can be easily deployed in practice since it just involves collecting a small dataset of measurements at a few tens of locations that need not even be computed or recorded. The scheme is evaluated on real data collected for this purpose.

SD-PINN: Deep Learning based Spatially Dependent PDEs Recovery

The physics-informed neural network (PINN) is capable of recovering partial differential equation (PDE) coefficients that remain constant throughout the spatial domain directly from physical measurements. In this work, we propose a spatially dependent physics-informed neural network (SD-PINN), which enables the recovery of coefficients in spatially-dependent PDEs using a single neural network, eliminating the requirement for domain-specific physical expertise. The proposed method exhibits robustness to noise owing to the incorporation of physical constraints. It can also incorporate the low-rank assumption of the spatial variation for the PDE coefficients to recover the coefficients at locations without available measurements.

Spoofing Attack Detection in the Physical Layer with Commutative Neural Networks

In a spoofing attack, an attacker impersonates a legitimate user to access or tamper with data intended for or produced by the legitimate user. In wireless communication systems, these attacks may be detected by relying on features of the channel and transmitter radios. In this context, a popular approach is to exploit the dependence of the received signal strength (RSS) at multiple receivers or access points with respect to the spatial location of the transmitter. Existing schemes rely on long-term estimates, which makes it difficult to distinguish spoofing from movement of a legitimate user. This limitation is here addressed by means of a deep neural network that implicitly learns the distribution of pairs of short-term RSS vector estimates. The adopted network architecture imposes the invariance to permutations of the input (commutativity) that the decision problem exhibits. The merits of the proposed algorithm are corroborated on a data set that we collected.

Deep Learning Object Detection Approaches to Signal Identification

Traditionally source identification is solved using threshold based energy detection algorithms. These algorithms frequently sum up the activity in regions, and consider regions above a specific activity threshold to be sources. While these algorithms work for the majority of cases, they often fail to detect signals that occupy small frequency bands, fail to distinguish sources with overlapping frequency bands, and cannot detect any signals under a specified signal to noise ratio. Through the conversion of raw signal data to spectrogram, source identification can be framed as an object detection problem. By leveraging modern advancements in deep learning based object detection, we propose a system that manages to alleviate the failure cases encountered when using traditional source identification algorithms. Our contributions include framing source identification as an object detection problem, the publication of a spectrogram object detection dataset, and evaluation of the RetinaNet and YOLOv5 object detection models trained on the dataset. Our final models achieve Mean Average Precisions of up to 0.906. With such a high Mean Average Precision, these models are sufficiently robust for use in real world applications.

Graph-Based Estimation of Time-Varying DOAs

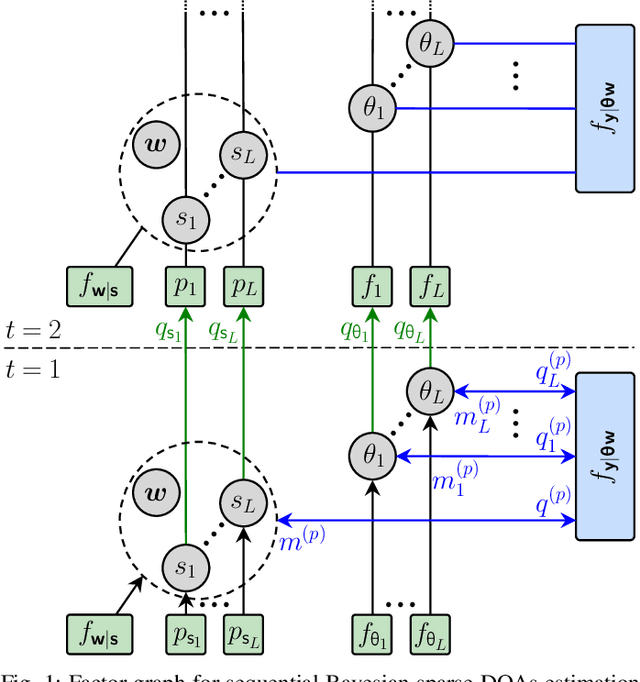
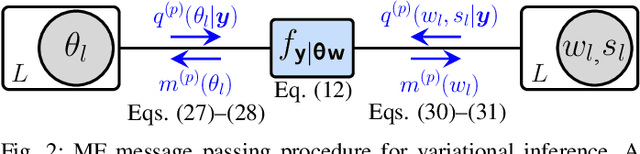
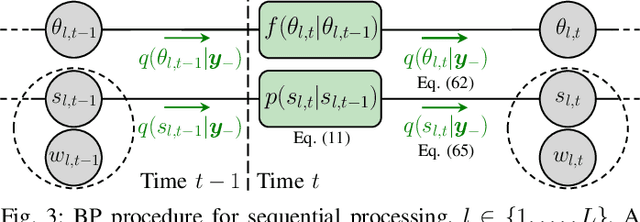
This paper presents a graph-based estimation method for sequential direction finding. The proposed method estimates an unknown number of directions of arrivals (DOAs) by performing message passing on the factor graph that represents the statistical model of the estimation problem. At each time step, belief propagation predicts the number of DOAs and their DOAs based on a new state-transition model and utilizing posterior probability density functions from previous time steps. Mean field message passing updates the DOAs and their number iteratively. The method promotes sparse solutions through a Bernoulli-Gaussian amplitude model, is gridless, and provides marginal posterior probability density functions from which DOA estimates and their uncertainties can be extracted. To propagate source existence and DOA information across time steps, a Bernoulli-von Mises state transition model is introduced. Compared to non-sequential approaches, the method can reduce DOA estimation errors in scenarios involving multiple time steps and time-varying DOAs. Simulation results demonstrate performance improvements compared to state-of-the-art methods. We evaluate the proposed method using ocean acoustic experimental data.