Graph-Based Estimation of Time-Varying DOAs

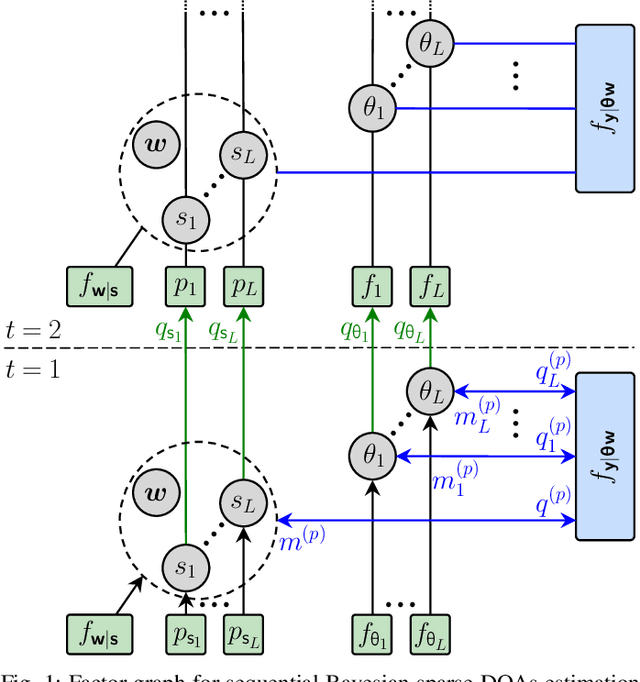
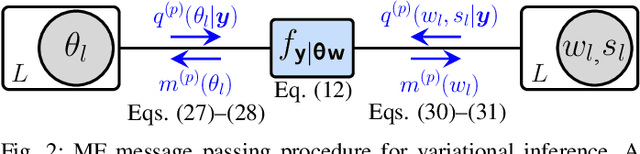
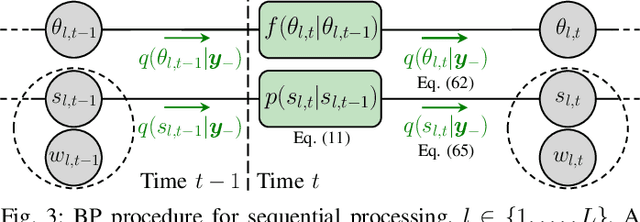
This paper presents a graph-based estimation method for sequential direction finding. The proposed method estimates an unknown number of directions of arrivals (DOAs) by performing message passing on the factor graph that represents the statistical model of the estimation problem. At each time step, belief propagation predicts the number of DOAs and their DOAs based on a new state-transition model and utilizing posterior probability density functions from previous time steps. Mean field message passing updates the DOAs and their number iteratively. The method promotes sparse solutions through a Bernoulli-Gaussian amplitude model, is gridless, and provides marginal posterior probability density functions from which DOA estimates and their uncertainties can be extracted. To propagate source existence and DOA information across time steps, a Bernoulli-von Mises state transition model is introduced. Compared to non-sequential approaches, the method can reduce DOA estimation errors in scenarios involving multiple time steps and time-varying DOAs. Simulation results demonstrate performance improvements compared to state-of-the-art methods. We evaluate the proposed method using ocean acoustic experimental data.