Scaling Continuous Kernels with Sparse Fourier Domain Learning
Paper and Code
Sep 15, 2024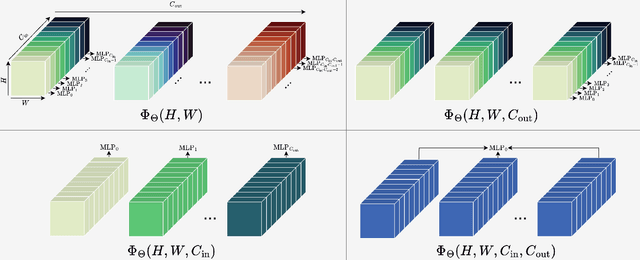

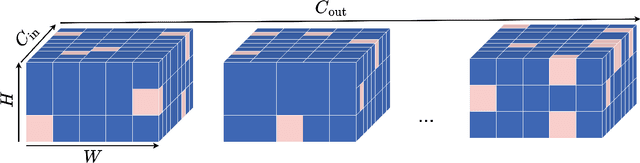

We address three key challenges in learning continuous kernel representations: computational efficiency, parameter efficiency, and spectral bias. Continuous kernels have shown significant potential, but their practical adoption is often limited by high computational and memory demands. Additionally, these methods are prone to spectral bias, which impedes their ability to capture high-frequency details. To overcome these limitations, we propose a novel approach that leverages sparse learning in the Fourier domain. Our method enables the efficient scaling of continuous kernels, drastically reduces computational and memory requirements, and mitigates spectral bias by exploiting the Gibbs phenomenon.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge