Marc Andrew Valdez
Department of Electrical Engineering, Colorado School of Mines, National Institute of Standards and Technology
On Grid Compressive Sensing for Spherical Field Measurements in Acoustics
Jun 22, 2022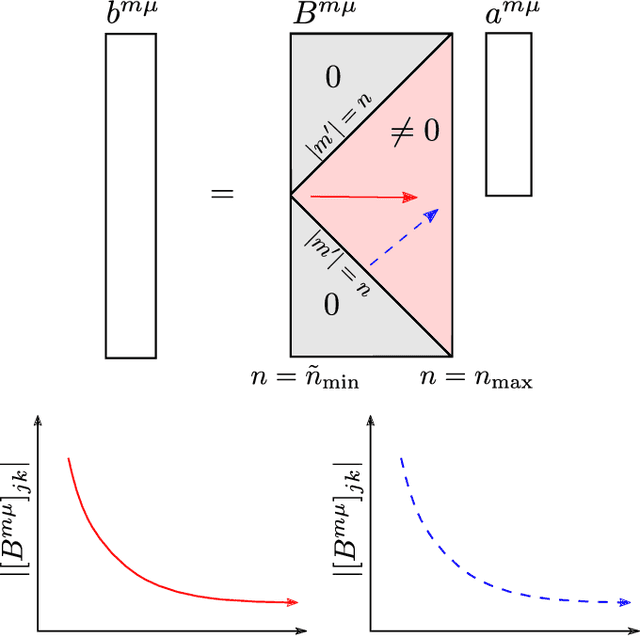
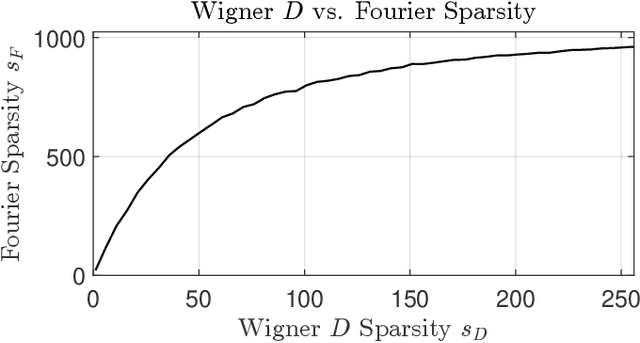
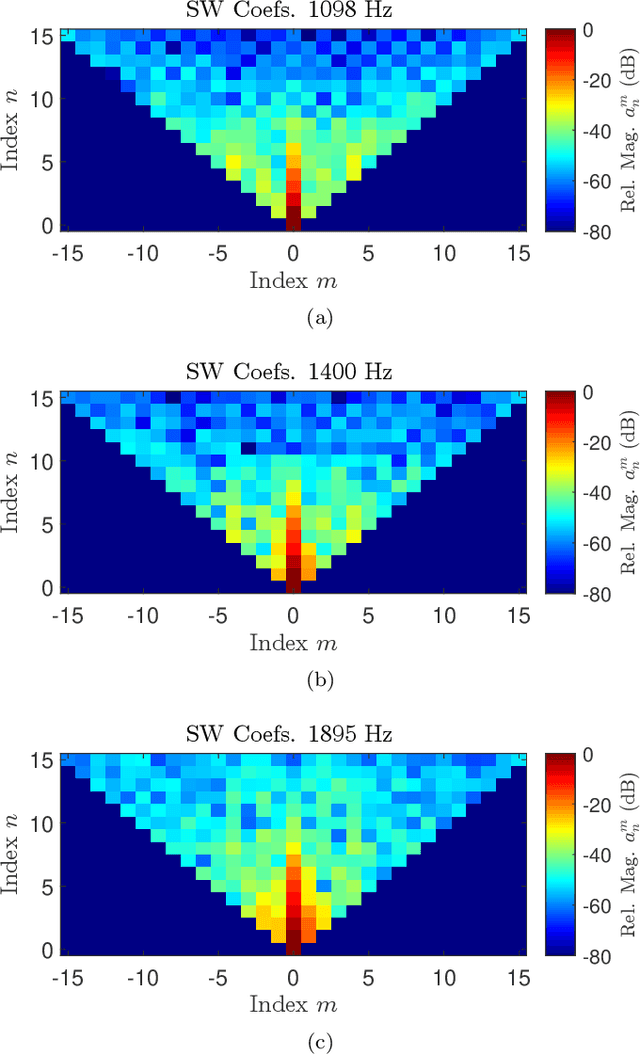
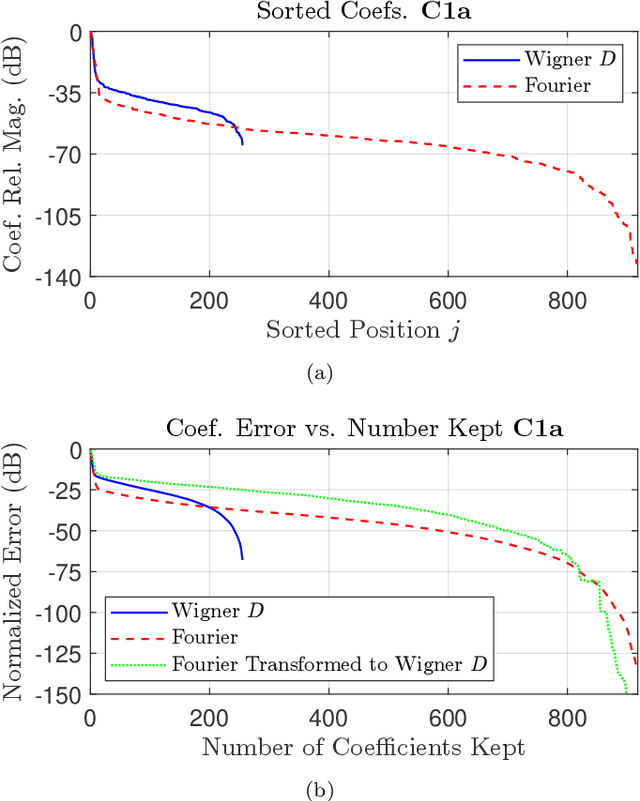
Abstract:We derive a theoretically guaranteed compressive sensing method for acoustic field reconstructions using spherical field measurements on a predefined grid. This method can be used to reconstruct sparse band-limited spherical harmonic or Wigner $D$-function series. Contrasting typical compressive sensing methods for spherical harmonic or Wigner $D$-function series that use random measurements on the sphere or rotation group, the new method samples on an equiangular grid in those domains, which is a commonly used sampling pattern. Using the periodic extension of the Wigner $D$-functions, we transform the reconstruction of a Wigner $D$-function series (of which spherical harmonics are a special case) into a multi-dimensional Fourier domain reconstruction problem. We establish that this transformation maintains sparsity in cases of interest and provide numerical studies of the transformation's effect on sparsity. We also provide numerical studies of the reconstruction performance of the compressive sensing approach compared to classical Nyquist sampling. In the cases tested, we find accurate compressive sensing reconstructions need only a fraction of the measurements dictated by the Nyquist sampling theorem. Moreover, using one-third of the measurements or less, the compressive sensing method can provide over 20 dB more denoising capabilities than oversampling with classical Fourier theory.
Restricted Domain Compressive Sensing for Antenna Metrology
Jun 07, 2022
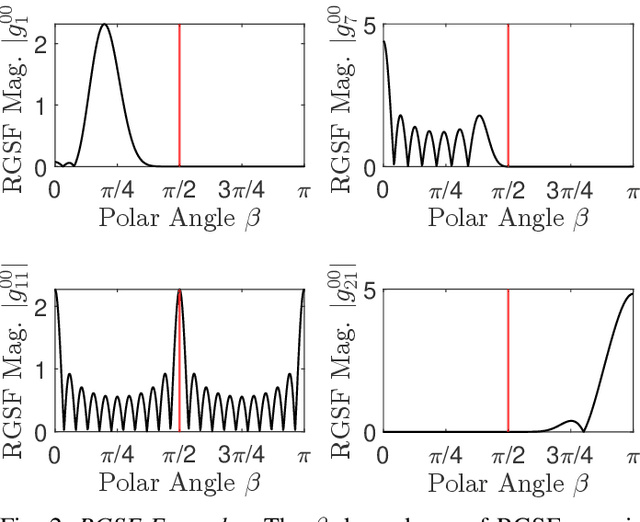
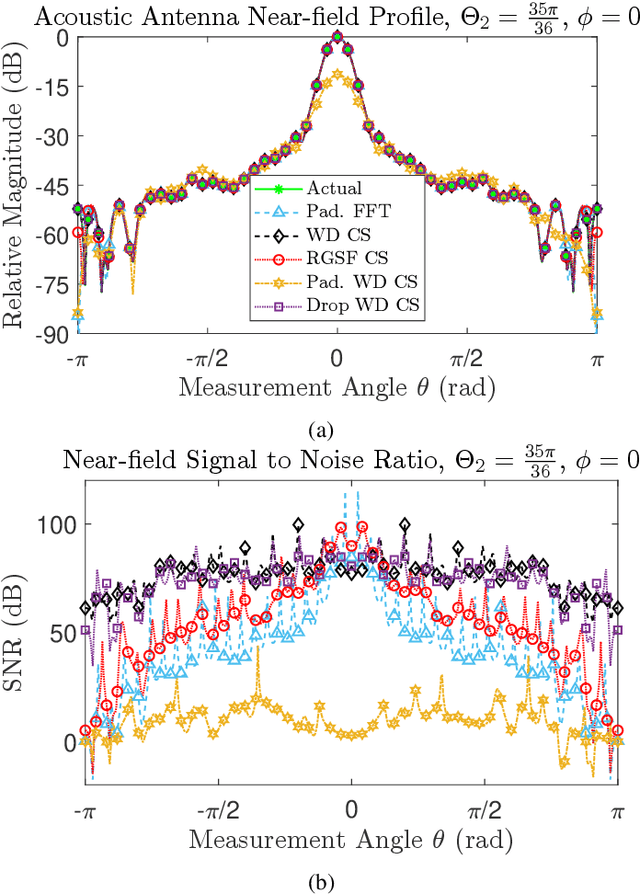
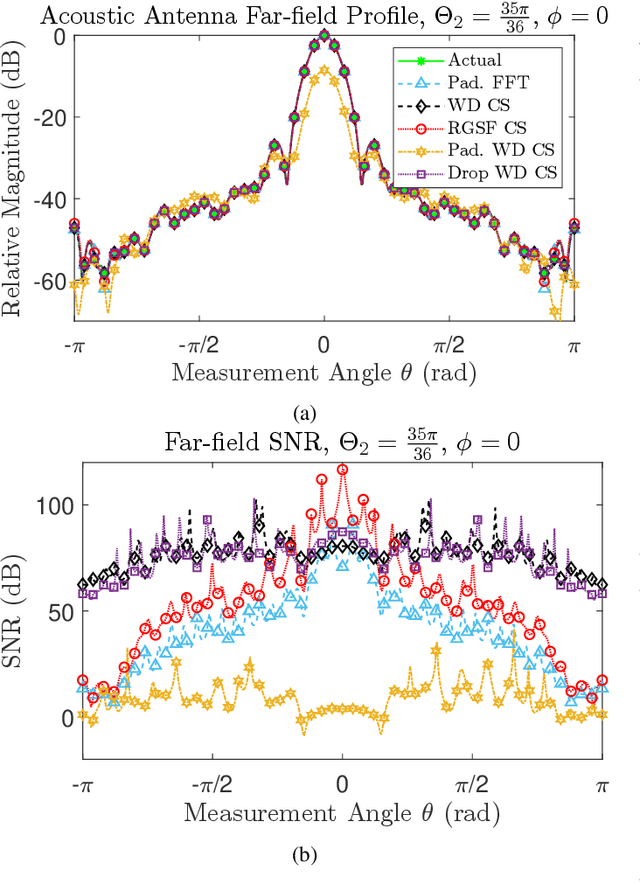
Abstract:In this paper, we prove a compressive sensing guarantee for restricted measurement domains in spherical near-field to far-field transformations for antenna metrology. We do so by first defining Slepian functions on a measurement sub-domain $R$ of the rotation group $\mathrm{SO}(3)$, the full domain of the linear inverse problem associated with spherical near-field to far-field transformations. Then, we transform the inverse problem from the measurement basis, the bounded orthonormal system of band-limited Wigner $D$-functions on $\mathrm{SO}(3)$, to the Slepian functions in a way that preserves sparsity. Contrasting methods using Wigner $D$-functions that require measurements on all of $\mathrm{SO}(3)$, we show that the orthogonality structure of the Slepian functions only requires measurements on the sub-domain $R$, which is select-able. Due to the particulars of this approach and the inherent presence of Slepian functions with low concentrations on $R$, our approach gives the highest accuracy when the signal under study is well concentrated on $R$. We provide numerical examples of our method in comparison with other classical and compressive sensing approaches. In terms of reconstruction quality, we find that our method outperforms the other compressive sensing approaches we test and is at least as good as classical approaches but with a significant reduction in the number of measurements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge