Designing Sparse Sensing Matrices for Image Compression

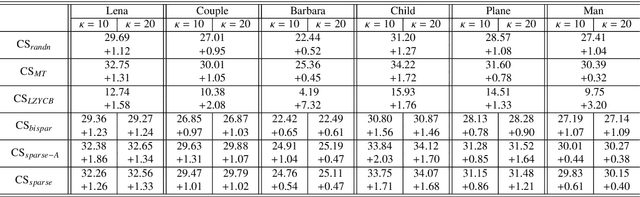
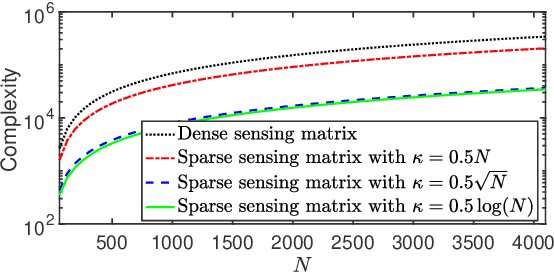
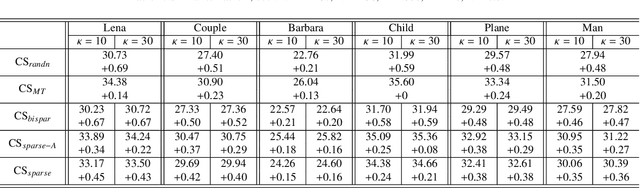
We consider designing a sparse sensing matrix which contains few non-zero entries per row and can be efficiently applied for capturing signals. The optimal sparse sensing matrix is designed so that it is also robust to sparse representation error of the signals and the Gram matrix of the equivalent dictionary is as close as possible to a target Gram matrix with small mutual coherence. An alternating minimization-based algorithm is proposed for solving the optimal design problem. We provide convergence analysis of the proposed algorithm which is proved to have sequence convergence, i.e., it generates a sequence that converges to a stationary point of the minimization problem. Experimental results show that the obtained sparse sensing matrix (even each row is extremely sparse) significantly outperforms a random dense sensing matrix in terms of signal reconstruction accuracy of synthetic data and peak signal-to-noise ratio (PSNR) for real images.