Projected Tensor-Tensor Products for Efficient Computation of Optimal Multiway Data Representations

Tensor decompositions have become essential tools for feature extraction and compression of multiway data. Recent advances in tensor operators have enabled desirable properties of standard matrix algebra to be retained for multilinear factorizations. Behind this matrix-mimetic tensor operation is an invertible matrix whose size depends quadratically on certain dimensions of the data. As a result, for large-scale multiway data, the invertible matrix can be computationally demanding to apply and invert and can lead to inefficient tensor representations in terms of construction and storage costs. In this work, we propose a new projected tensor-tensor product that relaxes the invertibility restriction to reduce computational overhead and still preserves fundamental linear algebraic properties. The transformation behind the projected product is a tall-and-skinny matrix with unitary columns, which depends only linearly on certain dimensions of the data, thereby reducing computational complexity by an order of magnitude. We provide extensive theory to prove the matrix mimeticity and the optimality of compressed representations within the projected product framework. We further prove that projected-product-based approximations outperform a comparable, non-matrix-mimetic tensor factorization. We support the theoretical findings and demonstrate the practical benefits of projected products through numerical experiments on video and hyperspectral imaging data.

Optimal Matrix-Mimetic Tensor Algebras via Variable Projection

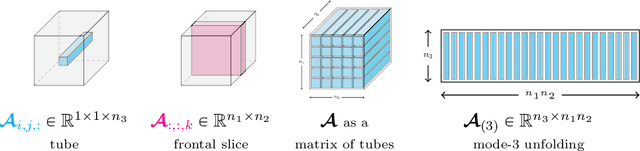
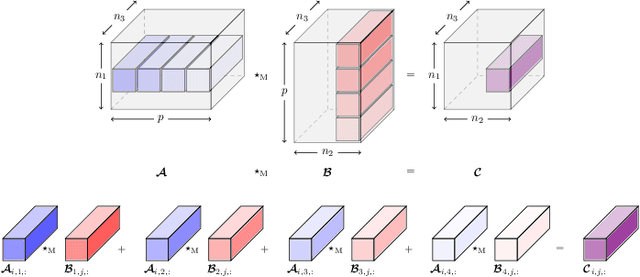
Recent advances in {matrix-mimetic} tensor frameworks have made it possible to preserve linear algebraic properties for multilinear data analysis and, as a result, to obtain optimal representations of multiway data. Matrix mimeticity arises from interpreting tensors as operators that can be multiplied, factorized, and analyzed analogous to matrices. Underlying the tensor operation is an algebraic framework parameterized by an invertible linear transformation. The choice of linear mapping is crucial to representation quality and, in practice, is made heuristically based on expected correlations in the data. However, in many cases, these correlations are unknown and common heuristics lead to suboptimal performance. In this work, we simultaneously learn optimal linear mappings and corresponding tensor representations without relying on prior knowledge of the data. Our new framework explicitly captures the coupling between the transformation and representation using variable projection. We preserve the invertibility of the linear mapping by learning orthogonal transformations with Riemannian optimization. We provide original theory of uniqueness of the transformation and convergence analysis of our variable-projection-based algorithm. We demonstrate the generality of our framework through numerical experiments on a wide range of applications, including financial index tracking, image compression, and reduced order modeling. We have published all the code related to this work at https://github.com/elizabethnewman/star-M-opt.

slimTrain -- A Stochastic Approximation Method for Training Separable Deep Neural Networks

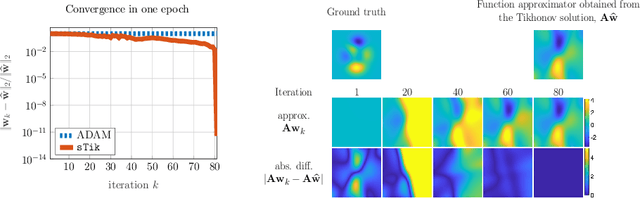
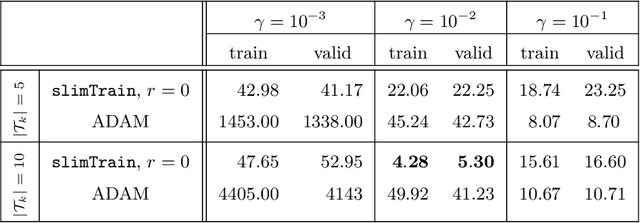
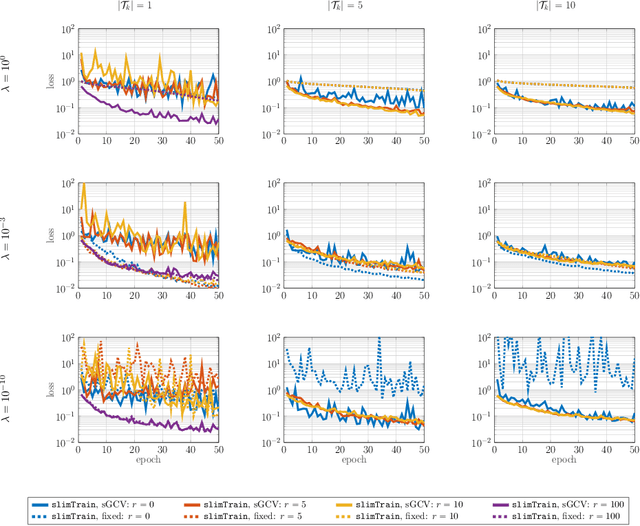
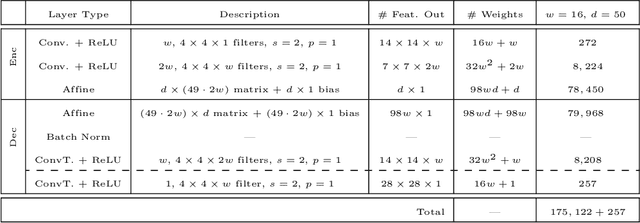
Deep neural networks (DNNs) have shown their success as high-dimensional function approximators in many applications; however, training DNNs can be challenging in general. DNN training is commonly phrased as a stochastic optimization problem whose challenges include non-convexity, non-smoothness, insufficient regularization, and complicated data distributions. Hence, the performance of DNNs on a given task depends crucially on tuning hyperparameters, especially learning rates and regularization parameters. In the absence of theoretical guidelines or prior experience on similar tasks, this requires solving many training problems, which can be time-consuming and demanding on computational resources. This can limit the applicability of DNNs to problems with non-standard, complex, and scarce datasets, e.g., those arising in many scientific applications. To remedy the challenges of DNN training, we propose slimTrain, a stochastic optimization method for training DNNs with reduced sensitivity to the choice hyperparameters and fast initial convergence. The central idea of slimTrain is to exploit the separability inherent in many DNN architectures; that is, we separate the DNN into a nonlinear feature extractor followed by a linear model. This separability allows us to leverage recent advances made for solving large-scale, linear, ill-posed inverse problems. Crucially, for the linear weights, slimTrain does not require a learning rate and automatically adapts the regularization parameter. Since our method operates on mini-batches, its computational overhead per iteration is modest. In our numerical experiments, slimTrain outperforms existing DNN training methods with the recommended hyperparameter settings and reduces the sensitivity of DNN training to the remaining hyperparameters.

Train Like a Pro: Efficient Training of Neural Networks with Variable Projection

Deep neural networks (DNNs) have achieved state-of-the-art performance across a variety of traditional machine learning tasks, e.g., speech recognition, image classification, and segmentation. The ability of DNNs to efficiently approximate high-dimensional functions has also motivated their use in scientific applications, e.g., to solve partial differential equations (PDE) and to generate surrogate models. In this paper, we consider the supervised training of DNNs, which arises in many of the above applications. We focus on the central problem of optimizing the weights of the given DNN such that it accurately approximates the relation between observed input and target data. Devising effective solvers for this optimization problem is notoriously challenging due to the large number of weights, non-convexity, data-sparsity, and non-trivial choice of hyperparameters. To solve the optimization problem more efficiently, we propose the use of variable projection (VarPro), a method originally designed for separable nonlinear least-squares problems. Our main contribution is the Gauss-Newton VarPro method (GNvpro) that extends the reach of the VarPro idea to non-quadratic objective functions, most notably, cross-entropy loss functions arising in classification. These extensions make GNvpro applicable to all training problems that involve a DNN whose last layer is an affine mapping, which is common in many state-of-the-art architectures. In numerical experiments from classification and surrogate modeling, GNvpro not only solves the optimization problem more efficiently but also yields DNNs that generalize better than commonly-used optimization schemes.

Non-negative Tensor Patch Dictionary Approaches for Image Compression and Deblurring Applications

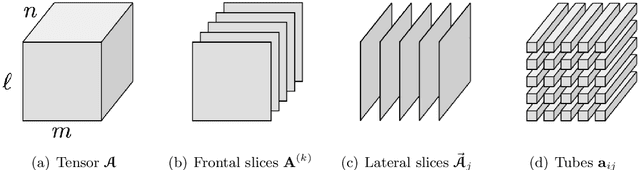
In recent work (Soltani, Kilmer, Hansen, BIT 2016), an algorithm for non-negative tensor patch dictionary learning in the context of X-ray CT imaging and based on a tensor-tensor product called the $t$-product (Kilmer and Martin, 2011) was presented. Building on that work, in this paper, we use of non-negative tensor patch-based dictionaries trained on other data, such as facial image data, for the purposes of either compression or image deblurring. We begin with an analysis in which we address issues such as suitability of the tensor-based approach relative to a matrix-based approach, dictionary size and patch size to balance computational efficiency and qualitative representations. Next, we develop an algorithm that is capable of recovering non-negative tensor coefficients given a non-negative tensor dictionary. The algorithm is based on a variant of the Modified Residual Norm Steepest Descent method. We show how to augment the algorithm to enforce sparsity in the tensor coefficients, and note that the approach has broader applicability since it can be applied to the matrix case as well. We illustrate the surprising result that dictionaries trained on image data from one class can be successfully used to represent and compress image data from different classes and across different resolutions. Finally, we address the use of non-negative tensor dictionaries in image deblurring. We show that tensor treatment of the deblurring problem coupled with non-negative tensor patch dictionaries can give superior restorations as compared to standard treatment of the non-negativity constrained deblurring problem.

Stable Tensor Neural Networks for Rapid Deep Learning

We propose a tensor neural network ($t$-NN) framework that offers an exciting new paradigm for designing neural networks with multidimensional (tensor) data. Our network architecture is based on the $t$-product (Kilmer and Martin, 2011), an algebraic formulation to multiply tensors via circulant convolution. In this $t$-product algebra, we interpret tensors as $t$-linear operators analogous to matrices as linear operators, and hence our framework inherits mimetic matrix properties. To exemplify the elegant, matrix-mimetic algebraic structure of our $t$-NNs, we expand on recent work (Haber and Ruthotto, 2017) which interprets deep neural networks as discretizations of non-linear differential equations and introduces stable neural networks which promote superior generalization. Motivated by this dynamic framework, we introduce a stable $t$-NN which facilitates more rapid learning because of its reduced, more powerful parameterization. Through our high-dimensional design, we create a more compact parameter space and extract multidimensional correlations otherwise latent in traditional algorithms. We further generalize our $t$-NN framework to a family of tensor-tensor products (Kernfeld, Kilmer, and Aeron, 2015) which still induce a matrix-mimetic algebraic structure. Through numerical experiments on the MNIST and CIFAR-10 datasets, we demonstrate the more powerful parameterizations and improved generalizability of stable $t$-NNs.

Image classification using local tensor singular value decompositions

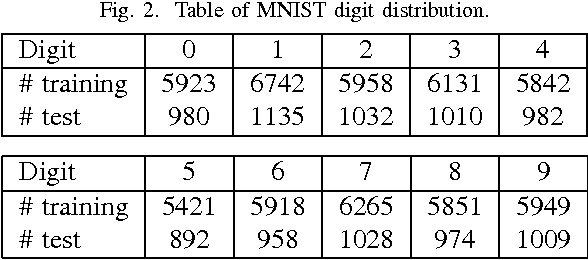
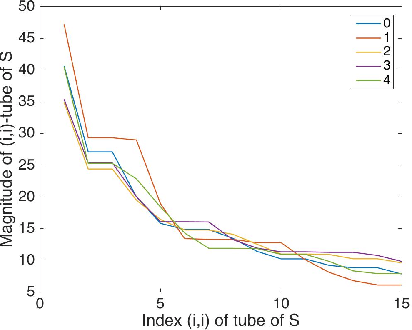
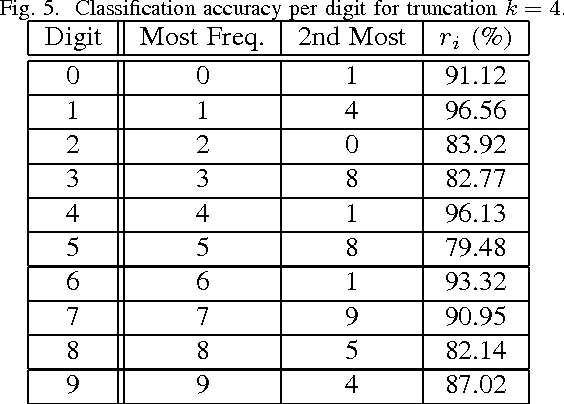
From linear classifiers to neural networks, image classification has been a widely explored topic in mathematics, and many algorithms have proven to be effective classifiers. However, the most accurate classifiers typically have significantly high storage costs, or require complicated procedures that may be computationally expensive. We present a novel (nonlinear) classification approach using truncation of local tensor singular value decompositions (tSVD) that robustly offers accurate results, while maintaining manageable storage costs. Our approach takes advantage of the optimality of the representation under the tensor algebra described to determine to which class an image belongs. We extend our approach to a method that can determine specific pairwise match scores, which could be useful in, for example, object recognition problems where pose/position are different. We demonstrate the promise of our new techniques on the MNIST data set.