Projected Tensor-Tensor Products for Efficient Computation of Optimal Multiway Data Representations

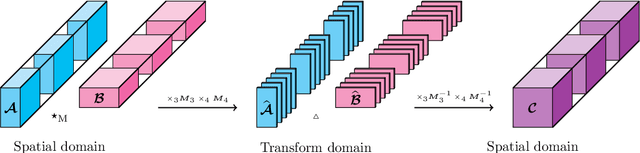
Tensor decompositions have become essential tools for feature extraction and compression of multiway data. Recent advances in tensor operators have enabled desirable properties of standard matrix algebra to be retained for multilinear factorizations. Behind this matrix-mimetic tensor operation is an invertible matrix whose size depends quadratically on certain dimensions of the data. As a result, for large-scale multiway data, the invertible matrix can be computationally demanding to apply and invert and can lead to inefficient tensor representations in terms of construction and storage costs. In this work, we propose a new projected tensor-tensor product that relaxes the invertibility restriction to reduce computational overhead and still preserves fundamental linear algebraic properties. The transformation behind the projected product is a tall-and-skinny matrix with unitary columns, which depends only linearly on certain dimensions of the data, thereby reducing computational complexity by an order of magnitude. We provide extensive theory to prove the matrix mimeticity and the optimality of compressed representations within the projected product framework. We further prove that projected-product-based approximations outperform a comparable, non-matrix-mimetic tensor factorization. We support the theoretical findings and demonstrate the practical benefits of projected products through numerical experiments on video and hyperspectral imaging data.

Optimal Matrix-Mimetic Tensor Algebras via Variable Projection

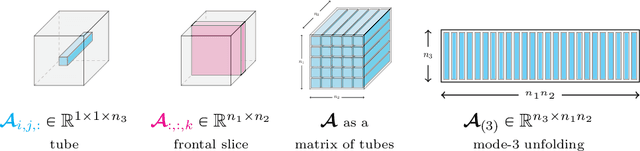
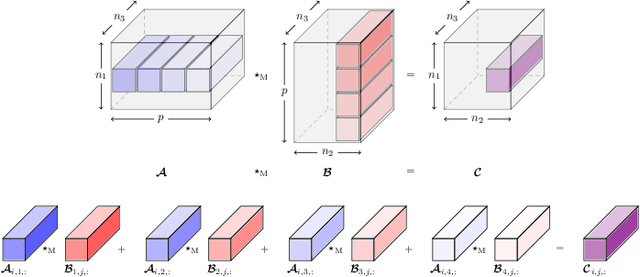
Recent advances in {matrix-mimetic} tensor frameworks have made it possible to preserve linear algebraic properties for multilinear data analysis and, as a result, to obtain optimal representations of multiway data. Matrix mimeticity arises from interpreting tensors as operators that can be multiplied, factorized, and analyzed analogous to matrices. Underlying the tensor operation is an algebraic framework parameterized by an invertible linear transformation. The choice of linear mapping is crucial to representation quality and, in practice, is made heuristically based on expected correlations in the data. However, in many cases, these correlations are unknown and common heuristics lead to suboptimal performance. In this work, we simultaneously learn optimal linear mappings and corresponding tensor representations without relying on prior knowledge of the data. Our new framework explicitly captures the coupling between the transformation and representation using variable projection. We preserve the invertibility of the linear mapping by learning orthogonal transformations with Riemannian optimization. We provide original theory of uniqueness of the transformation and convergence analysis of our variable-projection-based algorithm. We demonstrate the generality of our framework through numerical experiments on a wide range of applications, including financial index tracking, image compression, and reduced order modeling. We have published all the code related to this work at https://github.com/elizabethnewman/star-M-opt.

A Tensor SVD-based Classification Algorithm Applied to fMRI Data

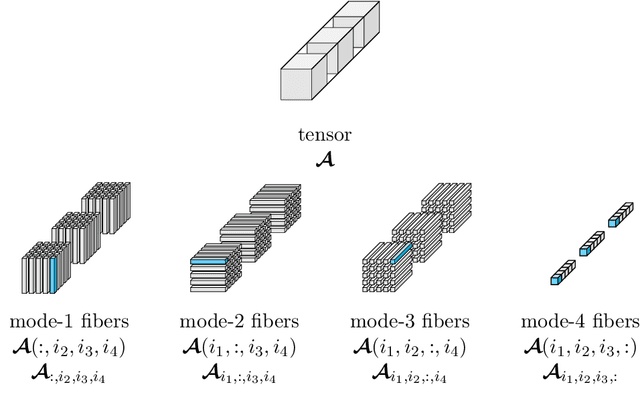
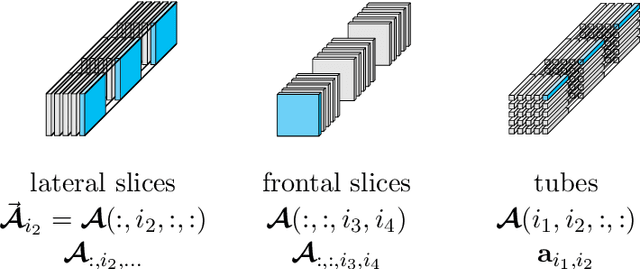
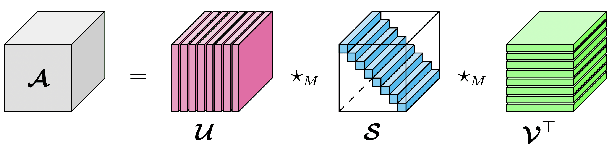
To analyze the abundance of multidimensional data, tensor-based frameworks have been developed. Traditionally, the matrix singular value decomposition (SVD) is used to extract the most dominant features from a matrix containing the vectorized data. While the SVD is highly useful for data that can be appropriately represented as a matrix, this step of vectorization causes us to lose the high-dimensional relationships intrinsic to the data. To facilitate efficient multidimensional feature extraction, we utilize a projection-based classification algorithm using the t-SVDM, a tensor analog of the matrix SVD. Our work extends the t-SVDM framework and the classification algorithm, both initially proposed for tensors of order 3, to any number of dimensions. We then apply this algorithm to a classification task using the StarPlus fMRI dataset. Our numerical experiments demonstrate that there exists a superior tensor-based approach to fMRI classification than the best possible equivalent matrix-based approach. Our results illustrate the advantages of our chosen tensor framework, provide insight into beneficial choices of parameters, and could be further developed for classification of more complex imaging data. We provide our Python implementation at https://github.com/elizabethnewman/tensor-fmri.