Parametric Level-sets Enhanced To Improve Reconstruction (PaLEnTIR)

In this paper, we consider the restoration and reconstruction of piecewise constant objects in two and three dimensions using PaLEnTIR, a significantly enhanced Parametric level set (PaLS) model relative to the current state-of-the-art. The primary contribution of this paper is a new PaLS formulation which requires only a single level set function to recover a scene with piecewise constant objects possessing multiple unknown contrasts. Our model offers distinct advantages over current approaches to the multi-contrast, multi-object problem, all of which require multiple level sets and explicit estimation of the contrast magnitudes. Given upper and lower bounds on the contrast, our approach is able to recover objects with any distribution of contrasts and eliminates the need to know either the number of contrasts in a given scene or their values. We provide an iterative process for finding these space-varying contrast limits. Relative to most PaLS methods which employ radial basis functions (RBFs), our model makes use of non-isotropic basis functions, thereby expanding the class of shapes that a PaLS model of a given complexity can approximate. Finally, PaLEnTIR improves the conditioning of the Jacobian matrix required as part of the parameter identification process and consequently accelerates the optimization methods by controlling the magnitude of the PaLS expansion coefficients, fixing the centers of the basis functions, and the uniqueness of parametric to image mappings provided by the new parameterization. We demonstrate the performance of the new approach using both 2D and 3D variants of X-ray computed tomography, diffuse optical tomography (DOT), denoising, deconvolution problems. Application to experimental sparse CT data and simulated data with different types of noise are performed to further validate the proposed method.

Stable Tensor Neural Networks for Rapid Deep Learning

We propose a tensor neural network ($t$-NN) framework that offers an exciting new paradigm for designing neural networks with multidimensional (tensor) data. Our network architecture is based on the $t$-product (Kilmer and Martin, 2011), an algebraic formulation to multiply tensors via circulant convolution. In this $t$-product algebra, we interpret tensors as $t$-linear operators analogous to matrices as linear operators, and hence our framework inherits mimetic matrix properties. To exemplify the elegant, matrix-mimetic algebraic structure of our $t$-NNs, we expand on recent work (Haber and Ruthotto, 2017) which interprets deep neural networks as discretizations of non-linear differential equations and introduces stable neural networks which promote superior generalization. Motivated by this dynamic framework, we introduce a stable $t$-NN which facilitates more rapid learning because of its reduced, more powerful parameterization. Through our high-dimensional design, we create a more compact parameter space and extract multidimensional correlations otherwise latent in traditional algorithms. We further generalize our $t$-NN framework to a family of tensor-tensor products (Kernfeld, Kilmer, and Aeron, 2015) which still induce a matrix-mimetic algebraic structure. Through numerical experiments on the MNIST and CIFAR-10 datasets, we demonstrate the more powerful parameterizations and improved generalizability of stable $t$-NNs.

Image classification using local tensor singular value decompositions

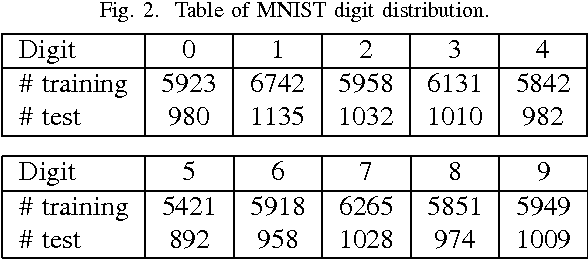
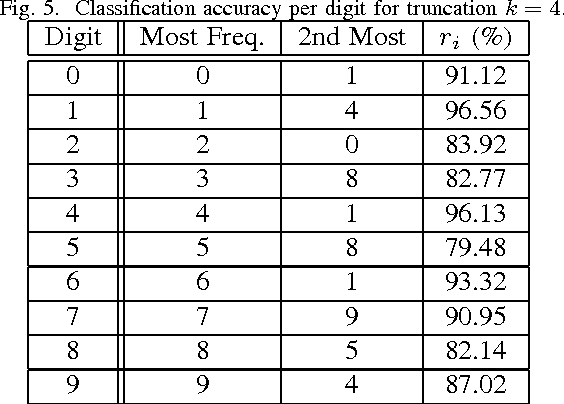
From linear classifiers to neural networks, image classification has been a widely explored topic in mathematics, and many algorithms have proven to be effective classifiers. However, the most accurate classifiers typically have significantly high storage costs, or require complicated procedures that may be computationally expensive. We present a novel (nonlinear) classification approach using truncation of local tensor singular value decompositions (tSVD) that robustly offers accurate results, while maintaining manageable storage costs. Our approach takes advantage of the optimality of the representation under the tensor algebra described to determine to which class an image belongs. We extend our approach to a method that can determine specific pairwise match scores, which could be useful in, for example, object recognition problems where pose/position are different. We demonstrate the promise of our new techniques on the MNIST data set.

Multilinear Subspace Clustering

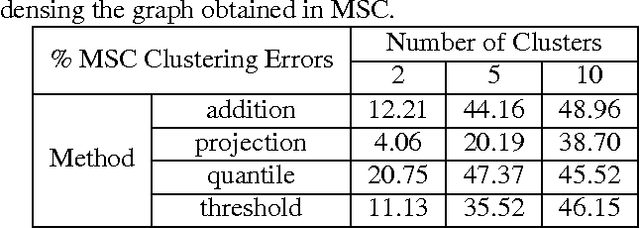
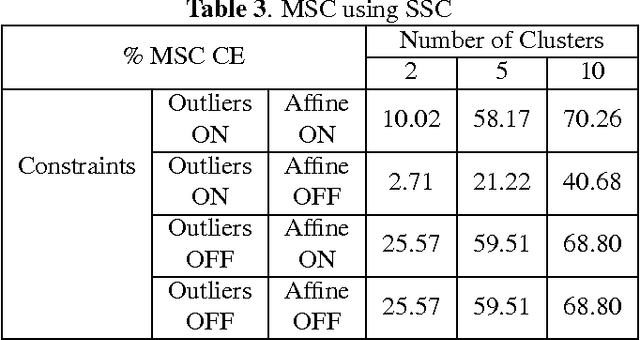
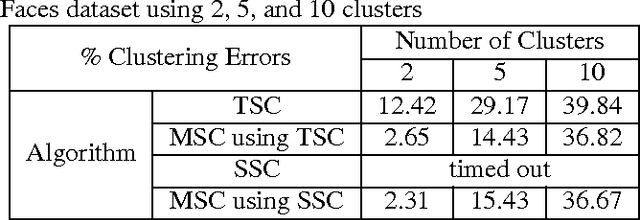
In this paper we present a new model and an algorithm for unsupervised clustering of 2-D data such as images. We assume that the data comes from a union of multilinear subspaces (UOMS) model, which is a specific structured case of the much studied union of subspaces (UOS) model. For segmentation under this model, we develop Multilinear Subspace Clustering (MSC) algorithm and evaluate its performance on the YaleB and Olivietti image data sets. We show that MSC is highly competitive with existing algorithms employing the UOS model in terms of clustering performance while enjoying improvement in computational complexity.

Clustering multi-way data: a novel algebraic approach

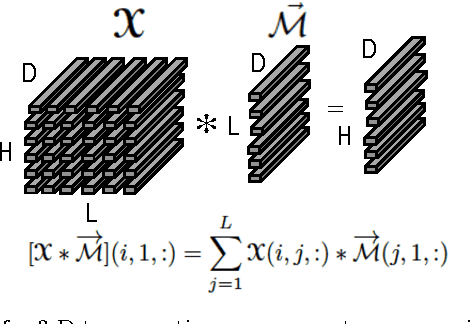
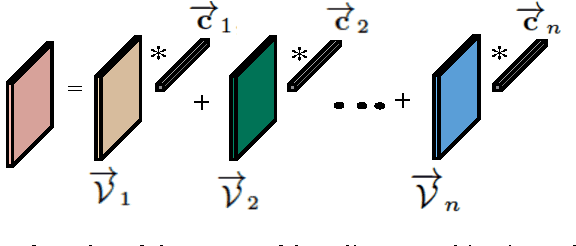
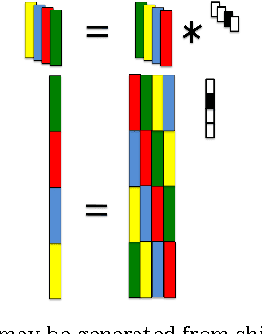
In this paper, we develop a method for unsupervised clustering of two-way (matrix) data by combining two recent innovations from different fields: the Sparse Subspace Clustering (SSC) algorithm [10], which groups points coming from a union of subspaces into their respective subspaces, and the t-product [18], which was introduced to provide a matrix-like multiplication for third order tensors. Our algorithm is analogous to SSC in that an "affinity" between different data points is built using a sparse self-representation of the data. Unlike SSC, we employ the t-product in the self-representation. This allows us more flexibility in modeling; infact, SSC is a special case of our method. When using the t-product, three-way arrays are treated as matrices whose elements (scalars) are n-tuples or tubes. Convolutions take the place of scalar multiplication. This framework allows us to embed the 2-D data into a vector-space-like structure called a free module over a commutative ring. These free modules retain many properties of complex inner-product spaces, and we leverage that to provide theoretical guarantees on our algorithm. We show that compared to vector-space counterparts, SSmC achieves higher accuracy and better able to cluster data with less preprocessing in some image clustering problems. In particular we show the performance of the proposed method on Weizmann face database, the Extended Yale B Face database and the MNIST handwritten digits database.

Novel methods for multilinear data completion and de-noising based on tensor-SVD

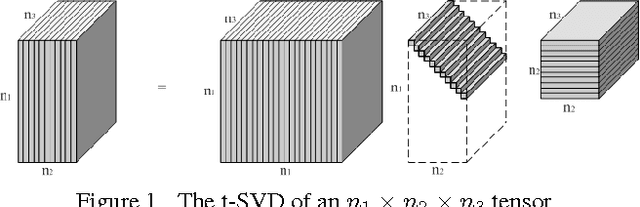
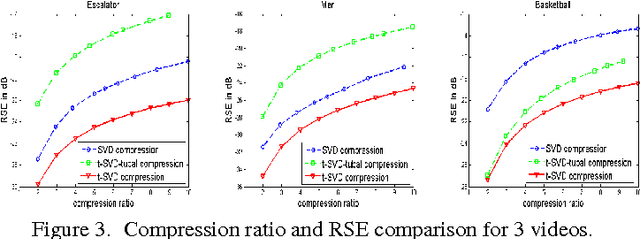
In this paper we propose novel methods for completion (from limited samples) and de-noising of multilinear (tensor) data and as an application consider 3-D and 4- D (color) video data completion and de-noising. We exploit the recently proposed tensor-Singular Value Decomposition (t-SVD)[11]. Based on t-SVD, the notion of multilinear rank and a related tensor nuclear norm was proposed in [11] to characterize informational and structural complexity of multilinear data. We first show that videos with linear camera motion can be represented more efficiently using t-SVD compared to the approaches based on vectorizing or flattening of the tensors. Since efficiency in representation implies efficiency in recovery, we outline a tensor nuclear norm penalized algorithm for video completion from missing entries. Application of the proposed algorithm for video recovery from missing entries is shown to yield a superior performance over existing methods. We also consider the problem of tensor robust Principal Component Analysis (PCA) for de-noising 3-D video data from sparse random corruptions. We show superior performance of our method compared to the matrix robust PCA adapted to this setting as proposed in [4].

Novel Factorization Strategies for Higher Order Tensors: Implications for Compression and Recovery of Multi-linear Data

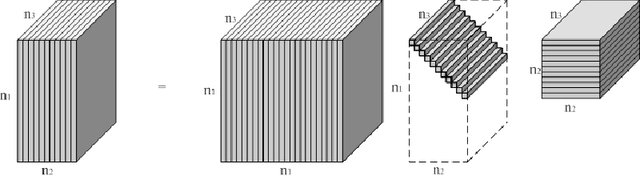
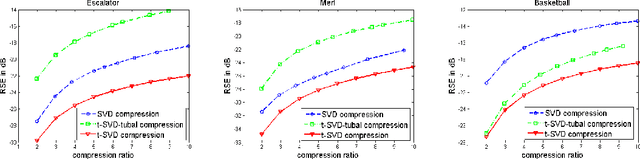
In this paper we propose novel methods for compression and recovery of multilinear data under limited sampling. We exploit the recently proposed tensor- Singular Value Decomposition (t-SVD)[1], which is a group theoretic framework for tensor decomposition. In contrast to popular existing tensor decomposition techniques such as higher-order SVD (HOSVD), t-SVD has optimality properties similar to the truncated SVD for matrices. Based on t-SVD, we first construct novel tensor-rank like measures to characterize informational and structural complexity of multilinear data. Following that we outline a complexity penalized algorithm for tensor completion from missing entries. As an application, 3-D and 4-D (color) video data compression and recovery are considered. We show that videos with linear camera motion can be represented more efficiently using t-SVD compared to traditional approaches based on vectorizing or flattening of the tensors. Application of the proposed tensor completion algorithm for video recovery from missing entries is shown to yield a superior performance over existing methods. In conclusion we point out several research directions and implications to online prediction of multilinear data.