Leveraging LLM Reasoning Enhances Personalized Recommender Systems

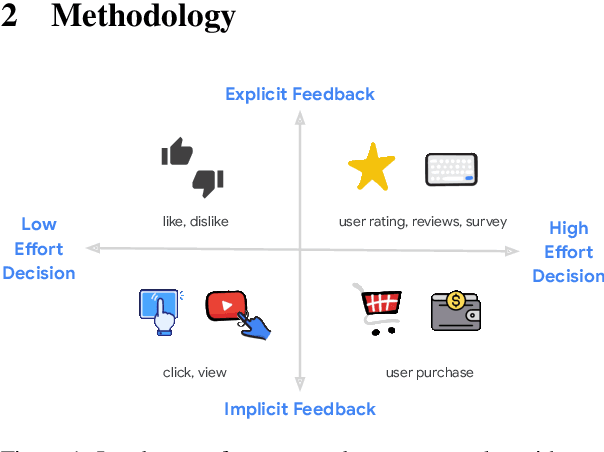
Recent advancements have showcased the potential of Large Language Models (LLMs) in executing reasoning tasks, particularly facilitated by Chain-of-Thought (CoT) prompting. While tasks like arithmetic reasoning involve clear, definitive answers and logical chains of thought, the application of LLM reasoning in recommendation systems (RecSys) presents a distinct challenge. RecSys tasks revolve around subjectivity and personalized preferences, an under-explored domain in utilizing LLMs' reasoning capabilities. Our study explores several aspects to better understand reasoning for RecSys and demonstrate how task quality improves by utilizing LLM reasoning in both zero-shot and finetuning settings. Additionally, we propose RecSAVER (Recommender Systems Automatic Verification and Evaluation of Reasoning) to automatically assess the quality of LLM reasoning responses without the requirement of curated gold references or human raters. We show that our framework aligns with real human judgment on the coherence and faithfulness of reasoning responses. Overall, our work shows that incorporating reasoning into RecSys can improve personalized tasks, paving the way for further advancements in recommender system methodologies.

Denoising and Completion of 3D Data via Multidimensional Dictionary Learning

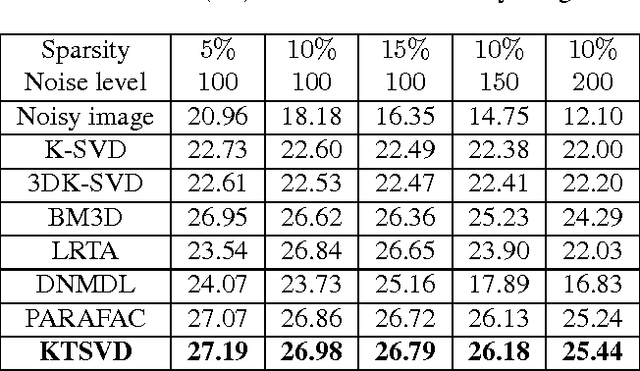
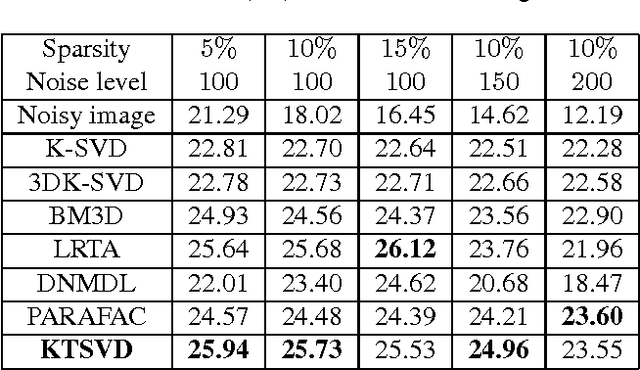
In this paper a new dictionary learning algorithm for multidimensional data is proposed. Unlike most conventional dictionary learning methods which are derived for dealing with vectors or matrices, our algorithm, named KTSVD, learns a multidimensional dictionary directly via a novel algebraic approach for tensor factorization as proposed in [3, 12, 13]. Using this approach one can define a tensor-SVD and we propose to extend K-SVD algorithm used for 1-D data to a K-TSVD algorithm for handling 2-D and 3-D data. Our algorithm, based on the idea of sparse coding (using group-sparsity over multidimensional coefficient vectors), alternates between estimating a compact representation and dictionary learning. We analyze our KTSVD algorithm and demonstrate its result on video completion and multispectral image denoising.

Exact tensor completion using t-SVD

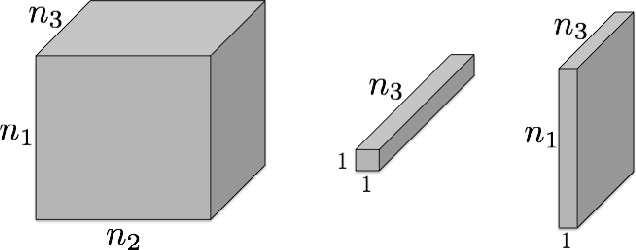
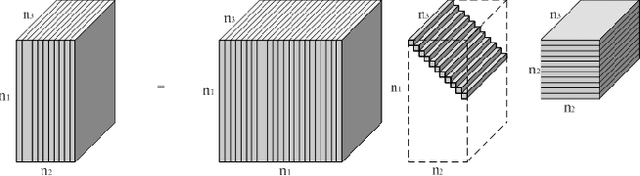
In this paper we focus on the problem of completion of multidimensional arrays (also referred to as tensors) from limited sampling. Our approach is based on a recently proposed tensor-Singular Value Decomposition (t-SVD) [1]. Using this factorization one can derive notion of tensor rank, referred to as the tensor tubal rank, which has optimality properties similar to that of matrix rank derived from SVD. As shown in [2] some multidimensional data, such as panning video sequences exhibit low tensor tubal rank and we look at the problem of completing such data under random sampling of the data cube. We show that by solving a convex optimization problem, which minimizes the tensor nuclear norm obtained as the convex relaxation of tensor tubal rank, one can guarantee recovery with overwhelming probability as long as samples in proportion to the degrees of freedom in t-SVD are observed. In this sense our results are order-wise optimal. The conditions under which this result holds are very similar to the incoherency conditions for the matrix completion, albeit we define incoherency under the algebraic set-up of t-SVD. We show the performance of the algorithm on some real data sets and compare it with other existing approaches based on tensor flattening and Tucker decomposition.

Novel methods for multilinear data completion and de-noising based on tensor-SVD

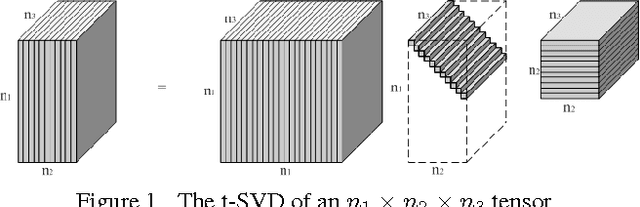
In this paper we propose novel methods for completion (from limited samples) and de-noising of multilinear (tensor) data and as an application consider 3-D and 4- D (color) video data completion and de-noising. We exploit the recently proposed tensor-Singular Value Decomposition (t-SVD)[11]. Based on t-SVD, the notion of multilinear rank and a related tensor nuclear norm was proposed in [11] to characterize informational and structural complexity of multilinear data. We first show that videos with linear camera motion can be represented more efficiently using t-SVD compared to the approaches based on vectorizing or flattening of the tensors. Since efficiency in representation implies efficiency in recovery, we outline a tensor nuclear norm penalized algorithm for video completion from missing entries. Application of the proposed algorithm for video recovery from missing entries is shown to yield a superior performance over existing methods. We also consider the problem of tensor robust Principal Component Analysis (PCA) for de-noising 3-D video data from sparse random corruptions. We show superior performance of our method compared to the matrix robust PCA adapted to this setting as proposed in [4].

Novel Factorization Strategies for Higher Order Tensors: Implications for Compression and Recovery of Multi-linear Data

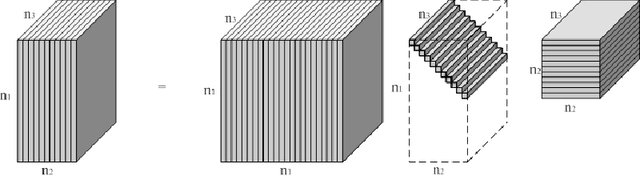
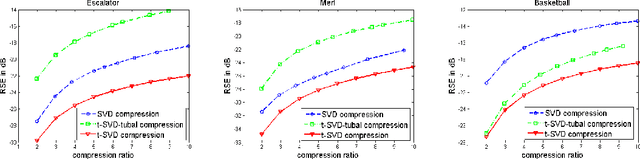
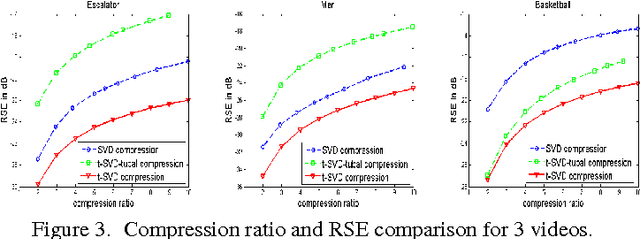
In this paper we propose novel methods for compression and recovery of multilinear data under limited sampling. We exploit the recently proposed tensor- Singular Value Decomposition (t-SVD)[1], which is a group theoretic framework for tensor decomposition. In contrast to popular existing tensor decomposition techniques such as higher-order SVD (HOSVD), t-SVD has optimality properties similar to the truncated SVD for matrices. Based on t-SVD, we first construct novel tensor-rank like measures to characterize informational and structural complexity of multilinear data. Following that we outline a complexity penalized algorithm for tensor completion from missing entries. As an application, 3-D and 4-D (color) video data compression and recovery are considered. We show that videos with linear camera motion can be represented more efficiently using t-SVD compared to traditional approaches based on vectorizing or flattening of the tensors. Application of the proposed tensor completion algorithm for video recovery from missing entries is shown to yield a superior performance over existing methods. In conclusion we point out several research directions and implications to online prediction of multilinear data.