Novel methods for multilinear data completion and de-noising based on tensor-SVD

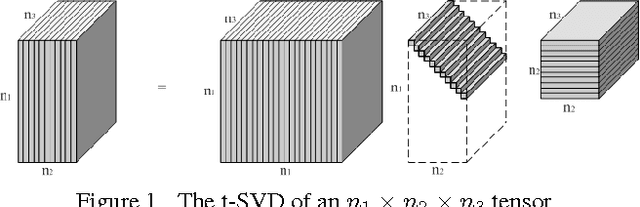
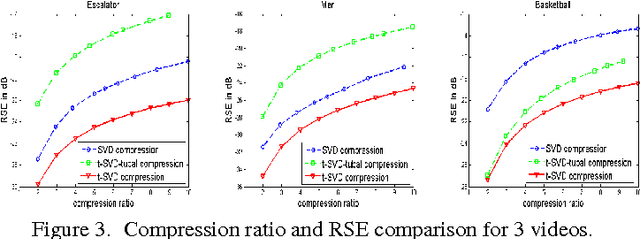
In this paper we propose novel methods for completion (from limited samples) and de-noising of multilinear (tensor) data and as an application consider 3-D and 4- D (color) video data completion and de-noising. We exploit the recently proposed tensor-Singular Value Decomposition (t-SVD)[11]. Based on t-SVD, the notion of multilinear rank and a related tensor nuclear norm was proposed in [11] to characterize informational and structural complexity of multilinear data. We first show that videos with linear camera motion can be represented more efficiently using t-SVD compared to the approaches based on vectorizing or flattening of the tensors. Since efficiency in representation implies efficiency in recovery, we outline a tensor nuclear norm penalized algorithm for video completion from missing entries. Application of the proposed algorithm for video recovery from missing entries is shown to yield a superior performance over existing methods. We also consider the problem of tensor robust Principal Component Analysis (PCA) for de-noising 3-D video data from sparse random corruptions. We show superior performance of our method compared to the matrix robust PCA adapted to this setting as proposed in [4].

Novel Factorization Strategies for Higher Order Tensors: Implications for Compression and Recovery of Multi-linear Data

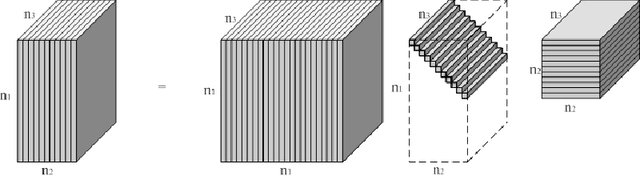
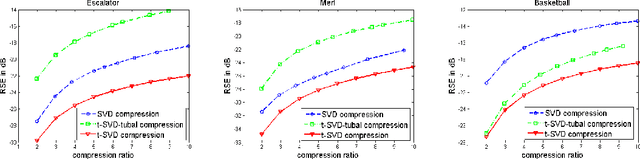
In this paper we propose novel methods for compression and recovery of multilinear data under limited sampling. We exploit the recently proposed tensor- Singular Value Decomposition (t-SVD)[1], which is a group theoretic framework for tensor decomposition. In contrast to popular existing tensor decomposition techniques such as higher-order SVD (HOSVD), t-SVD has optimality properties similar to the truncated SVD for matrices. Based on t-SVD, we first construct novel tensor-rank like measures to characterize informational and structural complexity of multilinear data. Following that we outline a complexity penalized algorithm for tensor completion from missing entries. As an application, 3-D and 4-D (color) video data compression and recovery are considered. We show that videos with linear camera motion can be represented more efficiently using t-SVD compared to traditional approaches based on vectorizing or flattening of the tensors. Application of the proposed tensor completion algorithm for video recovery from missing entries is shown to yield a superior performance over existing methods. In conclusion we point out several research directions and implications to online prediction of multilinear data.