Community Detection with Heterogeneous Block Covariance Model

Community detection is the task of clustering objects based on their pairwise relationships. Most of the model-based community detection methods, such as the stochastic block model and its variants, are designed for networks with binary (yes/no) edges. In many practical scenarios, edges often possess continuous weights, spanning positive and negative values, which reflect varying levels of connectivity. To address this challenge, we introduce the heterogeneous block covariance model (HBCM) that defines a community structure within the covariance matrix, where edges have signed and continuous weights. Furthermore, it takes into account the heterogeneity of objects when forming connections with other objects within a community. A novel variational expectation-maximization algorithm is proposed to estimate the group membership. The HBCM provides provable consistent estimates of memberships, and its promising performance is observed in numerical simulations with different setups. The model is applied to a single-cell RNA-seq dataset of a mouse embryo and a stock price dataset. Supplementary materials for this article are available online.

Distributed Consistent Multi-robot Cooperative Localization: A Coordinate Transformation Approach

This paper considers the problem of distributed cooperative localization (CL) via robot-to-robot measurements for a multi-robot system. We propose a distributed consistent CL algorithm. The key idea is to perform the EKF-based state estimation in a transformed coordinate system. Specifically, a coordinate transformation is constructed by decomposing the state-propagation Jacobian by which the correct observability properties are guaranteed. Moreover, the transformed state-propagation Jacobian becomes an identity matrix which is more suitable for distribution. In the proposed algorithm, a server-based framework is adopted to distributely estimate the robot pose in which each robot propagates its pose estimations and the server maintains the correlations. To reduce communication costs, only when the multi-robot system takes a robot-to-robot relative measurement, the robots and the server exchange information to update the pose estimations and the correlations. In addition, no assumptions are made about the type of robots or relative measurements. The proposed algorithm has been validated by experiments and shown to outperform the state-of-art algorithms in terms of consistency and accuracy.

KD-EKF: A Kalman Decomposition Based Extended Kalman Filter for Multi-Robot Cooperative Localization

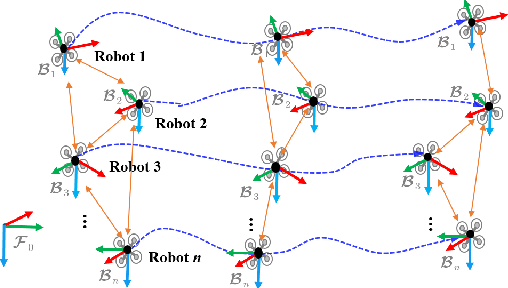
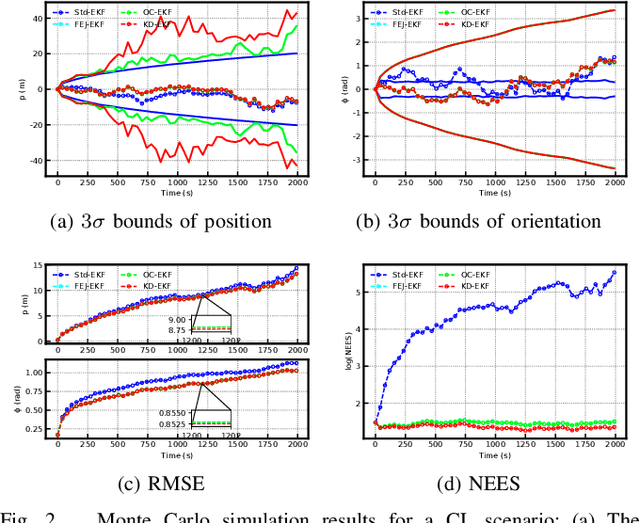
This paper investigates the consistency problem of EKF-based cooperative localization (CL) from the perspective of Kalman decomposition, which decomposes the observable and unobservable states and allows treating them individually. The factors causing the dimension reduction of the unobservable subspace, termed error discrepancy items, are explicitly isolated and identified in the state propagation and measurement Jacobians for the first time. We prove that the error discrepancy items lead to the global orientation being erroneously observable, which in turn causes the state estimation to be inconsistent. A CL algorithm, called Kalman decomposition-based EKF (KD-EKF), is proposed to improve consistency. The key idea is to perform state estimation using the Kalman observable canonical form in the transformed coordinates. By annihilating the error discrepancy items, proper observability properties are guaranteed. More importantly, the modified state propagation and measurement Jacobians are exactly equivalent to linearizing the nonlinear CL system at current best state estimates. Consequently, the inconsistency caused by the erroneous dimension reduction of the unobservable subspace is completely eliminated. The KD-EKF CL algorithm has been extensively verified in both Monte Carlo simulations and real-world experiments and shown to achieve better performance than state-of-the-art algorithms in terms of accuracy and consistency.

Variational Estimators of the Degree-corrected Latent Block Model for Bipartite Networks

Biclustering on bipartite graphs is an unsupervised learning task that simultaneously clusters the two types of objects in the graph, for example, users and movies in a movie review dataset. The latent block model (LBM) has been proposed as a model-based tool for biclustering. Biclustering results by the LBM are, however, usually dominated by the row and column sums of the data matrix, i.e., degrees. We propose a degree-corrected latent block model (DC-LBM) to accommodate degree heterogeneity in row and column clusters, which greatly outperforms the classical LBM in the MovieLens dataset and simulated data. We develop an efficient variational expectation-maximization algorithm by observing that the row and column degrees maximize the objective function in the M step given any probability assignment on the cluster labels. We prove the label consistency of the variational estimator under the DC-LBM, which allows the expected graph density goes to zero as long as the average expected degrees of rows and columns go to infinity.

Novel methods for multilinear data completion and de-noising based on tensor-SVD

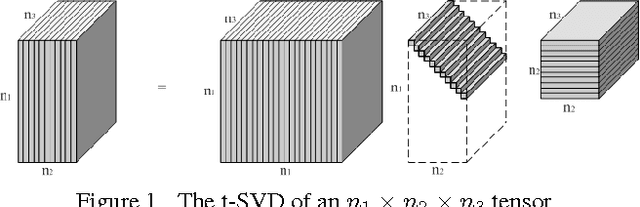
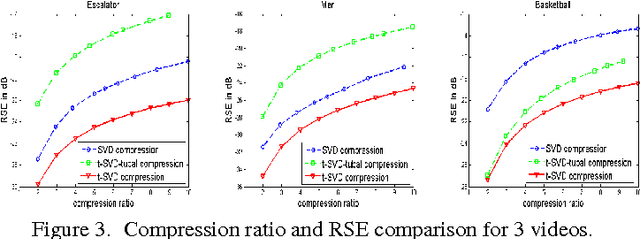
In this paper we propose novel methods for completion (from limited samples) and de-noising of multilinear (tensor) data and as an application consider 3-D and 4- D (color) video data completion and de-noising. We exploit the recently proposed tensor-Singular Value Decomposition (t-SVD)[11]. Based on t-SVD, the notion of multilinear rank and a related tensor nuclear norm was proposed in [11] to characterize informational and structural complexity of multilinear data. We first show that videos with linear camera motion can be represented more efficiently using t-SVD compared to the approaches based on vectorizing or flattening of the tensors. Since efficiency in representation implies efficiency in recovery, we outline a tensor nuclear norm penalized algorithm for video completion from missing entries. Application of the proposed algorithm for video recovery from missing entries is shown to yield a superior performance over existing methods. We also consider the problem of tensor robust Principal Component Analysis (PCA) for de-noising 3-D video data from sparse random corruptions. We show superior performance of our method compared to the matrix robust PCA adapted to this setting as proposed in [4].

Novel Factorization Strategies for Higher Order Tensors: Implications for Compression and Recovery of Multi-linear Data

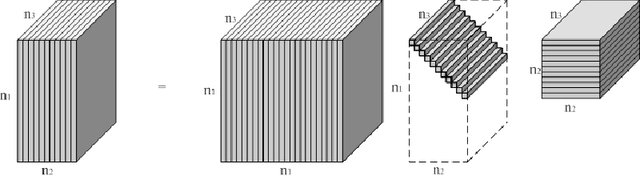
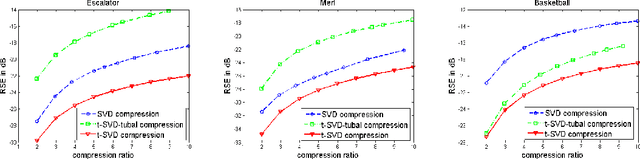
In this paper we propose novel methods for compression and recovery of multilinear data under limited sampling. We exploit the recently proposed tensor- Singular Value Decomposition (t-SVD)[1], which is a group theoretic framework for tensor decomposition. In contrast to popular existing tensor decomposition techniques such as higher-order SVD (HOSVD), t-SVD has optimality properties similar to the truncated SVD for matrices. Based on t-SVD, we first construct novel tensor-rank like measures to characterize informational and structural complexity of multilinear data. Following that we outline a complexity penalized algorithm for tensor completion from missing entries. As an application, 3-D and 4-D (color) video data compression and recovery are considered. We show that videos with linear camera motion can be represented more efficiently using t-SVD compared to traditional approaches based on vectorizing or flattening of the tensors. Application of the proposed tensor completion algorithm for video recovery from missing entries is shown to yield a superior performance over existing methods. In conclusion we point out several research directions and implications to online prediction of multilinear data.

Tensor-based formulation and nuclear norm regularization for multi-energy computed tomography

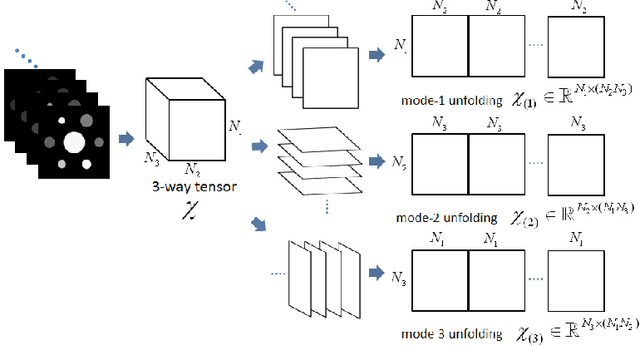
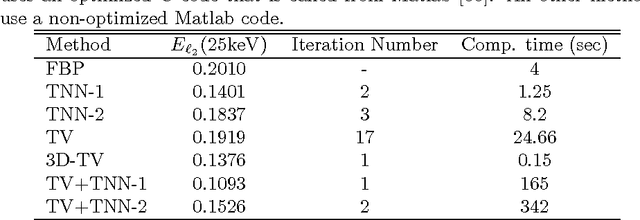
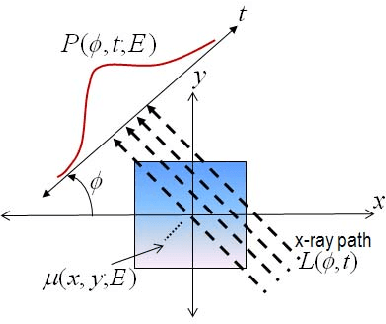
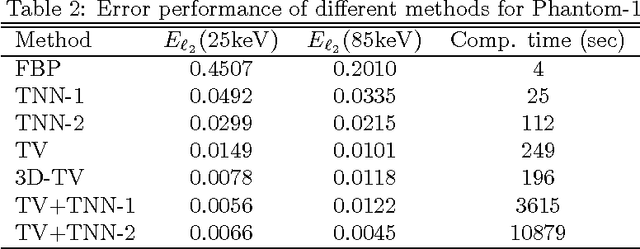
The development of energy selective, photon counting X-ray detectors allows for a wide range of new possibilities in the area of computed tomographic image formation. Under the assumption of perfect energy resolution, here we propose a tensor-based iterative algorithm that simultaneously reconstructs the X-ray attenuation distribution for each energy. We use a multi-linear image model rather than a more standard "stacked vector" representation in order to develop novel tensor-based regularizers. Specifically, we model the multi-spectral unknown as a 3-way tensor where the first two dimensions are space and the third dimension is energy. This approach allows for the design of tensor nuclear norm regularizers, which like its two dimensional counterpart, is a convex function of the multi-spectral unknown. The solution to the resulting convex optimization problem is obtained using an alternating direction method of multipliers (ADMM) approach. Simulation results shows that the generalized tensor nuclear norm can be used as a stand alone regularization technique for the energy selective (spectral) computed tomography (CT) problem and when combined with total variation regularization it enhances the regularization capabilities especially at low energy images where the effects of noise are most prominent.