Tensor-based formulation and nuclear norm regularization for multi-energy computed tomography
Paper and Code
Jul 19, 2013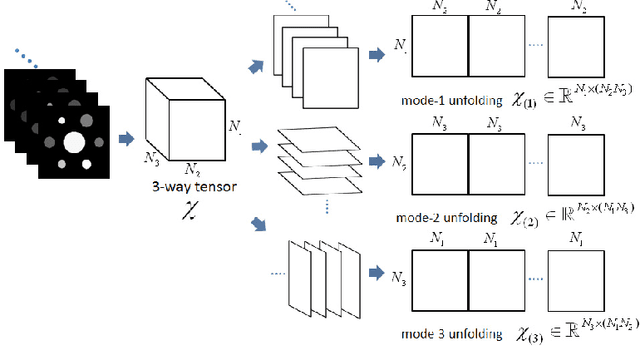
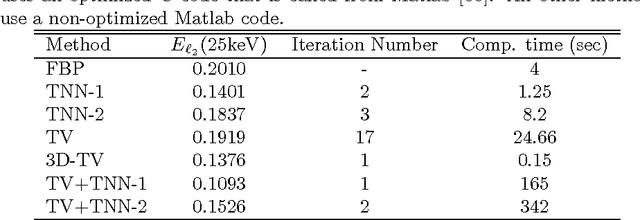
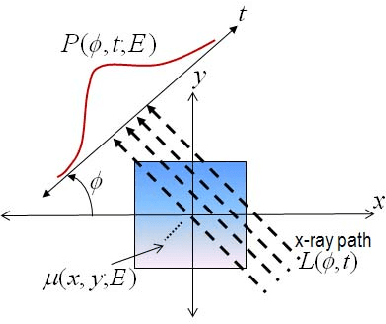
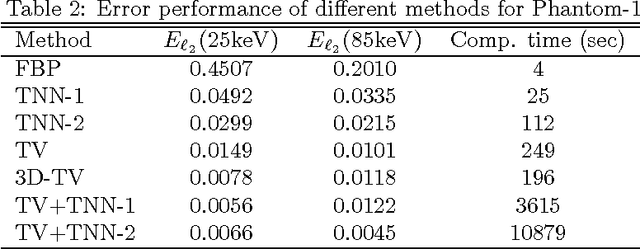
The development of energy selective, photon counting X-ray detectors allows for a wide range of new possibilities in the area of computed tomographic image formation. Under the assumption of perfect energy resolution, here we propose a tensor-based iterative algorithm that simultaneously reconstructs the X-ray attenuation distribution for each energy. We use a multi-linear image model rather than a more standard "stacked vector" representation in order to develop novel tensor-based regularizers. Specifically, we model the multi-spectral unknown as a 3-way tensor where the first two dimensions are space and the third dimension is energy. This approach allows for the design of tensor nuclear norm regularizers, which like its two dimensional counterpart, is a convex function of the multi-spectral unknown. The solution to the resulting convex optimization problem is obtained using an alternating direction method of multipliers (ADMM) approach. Simulation results shows that the generalized tensor nuclear norm can be used as a stand alone regularization technique for the energy selective (spectral) computed tomography (CT) problem and when combined with total variation regularization it enhances the regularization capabilities especially at low energy images where the effects of noise are most prominent.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge