Tensor Graph Convolutional Networks for Prediction on Dynamic Graphs

Many irregular domains such as social networks, financial transactions, neuron connections, and natural language structures are represented as graphs. In recent years, a variety of graph neural networks (GNNs) have been successfully applied for representation learning and prediction on such graphs. However, in many of the applications, the underlying graph changes over time and existing GNNs are inadequate for handling such dynamic graphs. In this paper we propose a novel technique for learning embeddings of dynamic graphs based on a tensor algebra framework. Our method extends the popular graph convolutional network (GCN) for learning representations of dynamic graphs using the recently proposed tensor M-product technique. Theoretical results that establish the connection between the proposed tensor approach and spectral convolution of tensors are developed. Numerical experiments on real datasets demonstrate the usefulness of the proposed method for an edge classification task on dynamic graphs.

Non-negative Tensor Patch Dictionary Approaches for Image Compression and Deblurring Applications

In recent work (Soltani, Kilmer, Hansen, BIT 2016), an algorithm for non-negative tensor patch dictionary learning in the context of X-ray CT imaging and based on a tensor-tensor product called the $t$-product (Kilmer and Martin, 2011) was presented. Building on that work, in this paper, we use of non-negative tensor patch-based dictionaries trained on other data, such as facial image data, for the purposes of either compression or image deblurring. We begin with an analysis in which we address issues such as suitability of the tensor-based approach relative to a matrix-based approach, dictionary size and patch size to balance computational efficiency and qualitative representations. Next, we develop an algorithm that is capable of recovering non-negative tensor coefficients given a non-negative tensor dictionary. The algorithm is based on a variant of the Modified Residual Norm Steepest Descent method. We show how to augment the algorithm to enforce sparsity in the tensor coefficients, and note that the approach has broader applicability since it can be applied to the matrix case as well. We illustrate the surprising result that dictionaries trained on image data from one class can be successfully used to represent and compress image data from different classes and across different resolutions. Finally, we address the use of non-negative tensor dictionaries in image deblurring. We show that tensor treatment of the deblurring problem coupled with non-negative tensor patch dictionaries can give superior restorations as compared to standard treatment of the non-negativity constrained deblurring problem.

A Tensor-Based Dictionary Learning Approach to Tomographic Image Reconstruction

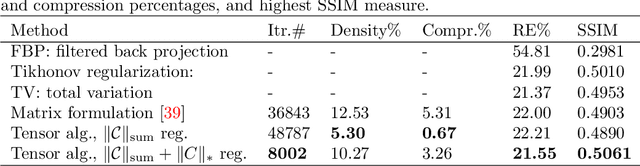
We consider tomographic reconstruction using priors in the form of a dictionary learned from training images. The reconstruction has two stages: first we construct a tensor dictionary prior from our training data, and then we pose the reconstruction problem in terms of recovering the expansion coefficients in that dictionary. Our approach differs from past approaches in that a) we use a third-order tensor representation for our images and b) we recast the reconstruction problem using the tensor formulation. The dictionary learning problem is presented as a non-negative tensor factorization problem with sparsity constraints. The reconstruction problem is formulated in a convex optimization framework by looking for a solution with a sparse representation in the tensor dictionary. Numerical results show that our tensor formulation leads to very sparse representations of both the training images and the reconstructions due to the ability of representing repeated features compactly in the dictionary.

Tensor-based formulation and nuclear norm regularization for multi-energy computed tomography

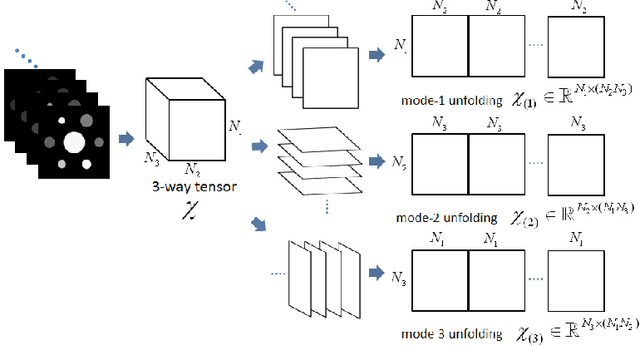
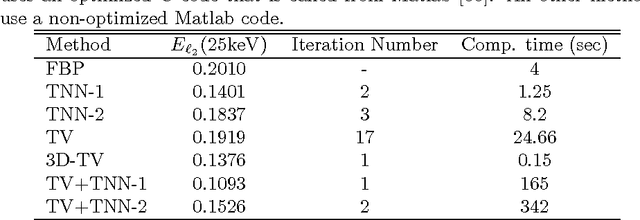
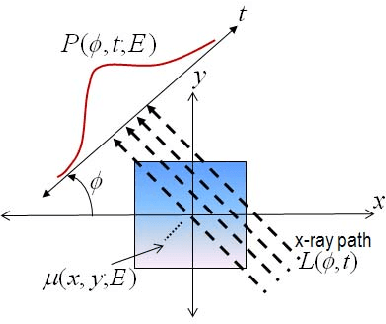
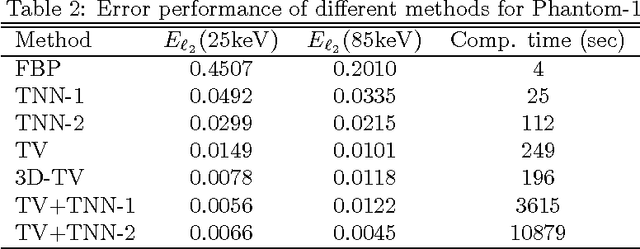
The development of energy selective, photon counting X-ray detectors allows for a wide range of new possibilities in the area of computed tomographic image formation. Under the assumption of perfect energy resolution, here we propose a tensor-based iterative algorithm that simultaneously reconstructs the X-ray attenuation distribution for each energy. We use a multi-linear image model rather than a more standard "stacked vector" representation in order to develop novel tensor-based regularizers. Specifically, we model the multi-spectral unknown as a 3-way tensor where the first two dimensions are space and the third dimension is energy. This approach allows for the design of tensor nuclear norm regularizers, which like its two dimensional counterpart, is a convex function of the multi-spectral unknown. The solution to the resulting convex optimization problem is obtained using an alternating direction method of multipliers (ADMM) approach. Simulation results shows that the generalized tensor nuclear norm can be used as a stand alone regularization technique for the energy selective (spectral) computed tomography (CT) problem and when combined with total variation regularization it enhances the regularization capabilities especially at low energy images where the effects of noise are most prominent.