Tensor Graph Convolutional Networks for Prediction on Dynamic Graphs
Paper and Code
Oct 16, 2019

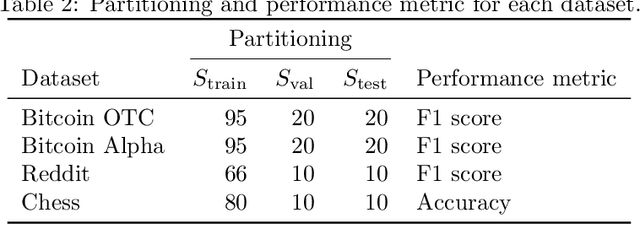
Many irregular domains such as social networks, financial transactions, neuron connections, and natural language structures are represented as graphs. In recent years, a variety of graph neural networks (GNNs) have been successfully applied for representation learning and prediction on such graphs. However, in many of the applications, the underlying graph changes over time and existing GNNs are inadequate for handling such dynamic graphs. In this paper we propose a novel technique for learning embeddings of dynamic graphs based on a tensor algebra framework. Our method extends the popular graph convolutional network (GCN) for learning representations of dynamic graphs using the recently proposed tensor M-product technique. Theoretical results that establish the connection between the proposed tensor approach and spectral convolution of tensors are developed. Numerical experiments on real datasets demonstrate the usefulness of the proposed method for an edge classification task on dynamic graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge