Tomographic Image Reconstruction using Training images

We describe and examine an algorithm for tomographic image reconstruction where prior knowledge about the solution is available in the form of training images. We first construct a nonnegative dictionary based on prototype elements from the training images; this problem is formulated as a regularized non-negative matrix factorization. Incorporating the dictionary as a prior in a convex reconstruction problem, we then find an approximate solution with a sparse representation in the dictionary. The dictionary is applied to non-overlapping patches of the image, which reduces the computational complexity compared to other algorithms. Computational experiments clarify the choice and interplay of the model parameters and the regularization parameters, and we show that in few-projection low-dose settings our algorithm is competitive with total variation regularization and tends to include more texture and more correct edges.

A Tensor-Based Dictionary Learning Approach to Tomographic Image Reconstruction

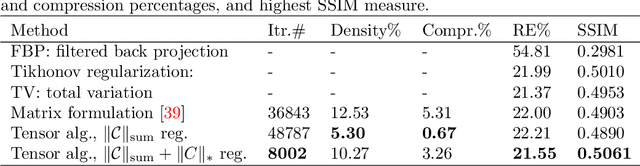
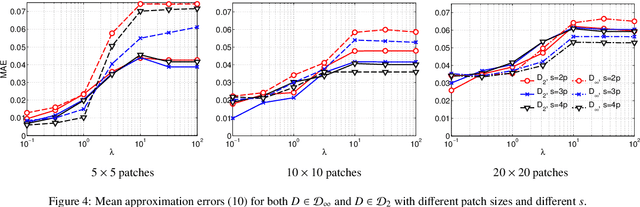
We consider tomographic reconstruction using priors in the form of a dictionary learned from training images. The reconstruction has two stages: first we construct a tensor dictionary prior from our training data, and then we pose the reconstruction problem in terms of recovering the expansion coefficients in that dictionary. Our approach differs from past approaches in that a) we use a third-order tensor representation for our images and b) we recast the reconstruction problem using the tensor formulation. The dictionary learning problem is presented as a non-negative tensor factorization problem with sparsity constraints. The reconstruction problem is formulated in a convex optimization framework by looking for a solution with a sparse representation in the tensor dictionary. Numerical results show that our tensor formulation leads to very sparse representations of both the training images and the reconstructions due to the ability of representing repeated features compactly in the dictionary.