AdaSub: Stochastic Optimization Using Second-Order Information in Low-Dimensional Subspaces

We introduce AdaSub, a stochastic optimization algorithm that computes a search direction based on second-order information in a low-dimensional subspace that is defined adaptively based on available current and past information. Compared to first-order methods, second-order methods exhibit better convergence characteristics, but the need to compute the Hessian matrix at each iteration results in excessive computational expenses, making them impractical. To address this issue, our approach enables the management of computational expenses and algorithm efficiency by enabling the selection of the subspace dimension for the search. Our code is freely available on GitHub, and our preliminary numerical results demonstrate that AdaSub surpasses popular stochastic optimizers in terms of time and number of iterations required to reach a given accuracy.

Regularization by Denoising Sub-sampled Newton Method for Spectral CT Multi-Material Decomposition

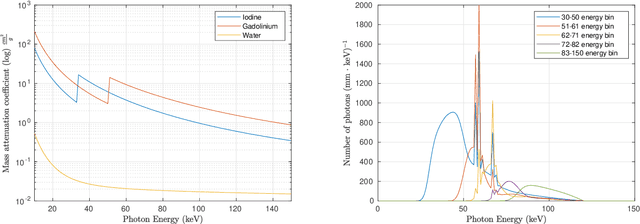
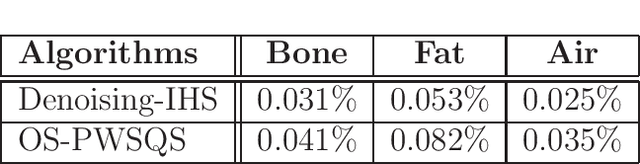
Spectral Computed Tomography (CT) is an emerging technology that enables to estimate the concentration of basis materials within a scanned object by exploiting different photon energy spectra. In this work, we aim at efficiently solving a model-based maximum-a-posterior problem to reconstruct multi-materials images with application to spectral CT. In particular, we propose to solve a regularized optimization problem based on a plug-in image-denoising function using a randomized second order method. By approximating the Newton step using a sketching of the Hessian of the likelihood function, it is possible to reduce the complexity while retaining the complex prior structure given by the data-driven regularizer. We exploit a non-uniform block sub-sampling of the Hessian with inexact but efficient Conjugate gradient updates that require only Jacobian-vector products for denoising term. Finally, we show numerical and experimental results for spectral CT materials decomposition.

Tomographic Image Reconstruction using Training images

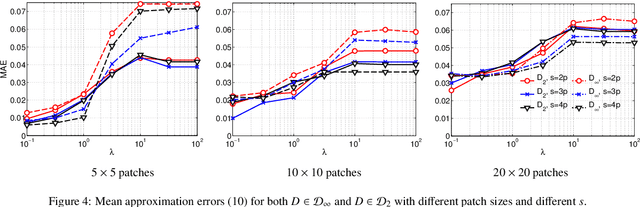
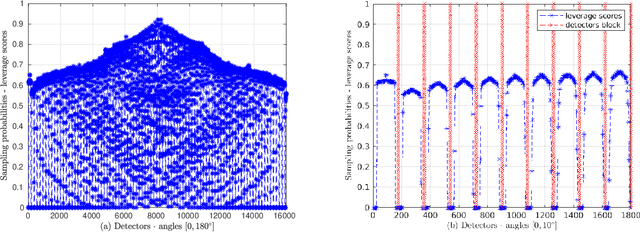
We describe and examine an algorithm for tomographic image reconstruction where prior knowledge about the solution is available in the form of training images. We first construct a nonnegative dictionary based on prototype elements from the training images; this problem is formulated as a regularized non-negative matrix factorization. Incorporating the dictionary as a prior in a convex reconstruction problem, we then find an approximate solution with a sparse representation in the dictionary. The dictionary is applied to non-overlapping patches of the image, which reduces the computational complexity compared to other algorithms. Computational experiments clarify the choice and interplay of the model parameters and the regularization parameters, and we show that in few-projection low-dose settings our algorithm is competitive with total variation regularization and tends to include more texture and more correct edges.