Tomographic Image Reconstruction using Training images
Paper and Code
Aug 17, 2015


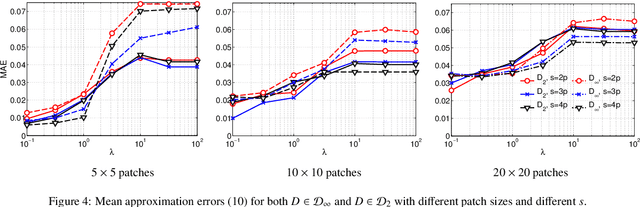
We describe and examine an algorithm for tomographic image reconstruction where prior knowledge about the solution is available in the form of training images. We first construct a nonnegative dictionary based on prototype elements from the training images; this problem is formulated as a regularized non-negative matrix factorization. Incorporating the dictionary as a prior in a convex reconstruction problem, we then find an approximate solution with a sparse representation in the dictionary. The dictionary is applied to non-overlapping patches of the image, which reduces the computational complexity compared to other algorithms. Computational experiments clarify the choice and interplay of the model parameters and the regularization parameters, and we show that in few-projection low-dose settings our algorithm is competitive with total variation regularization and tends to include more texture and more correct edges.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge