KD-EKF: A Kalman Decomposition Based Extended Kalman Filter for Multi-Robot Cooperative Localization
Paper and Code
Oct 28, 2022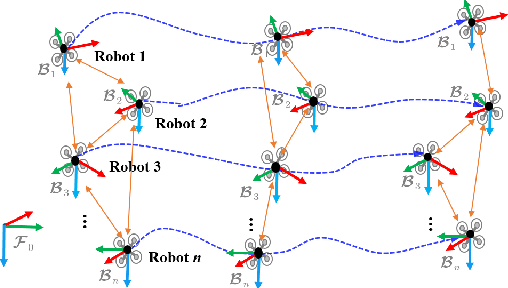
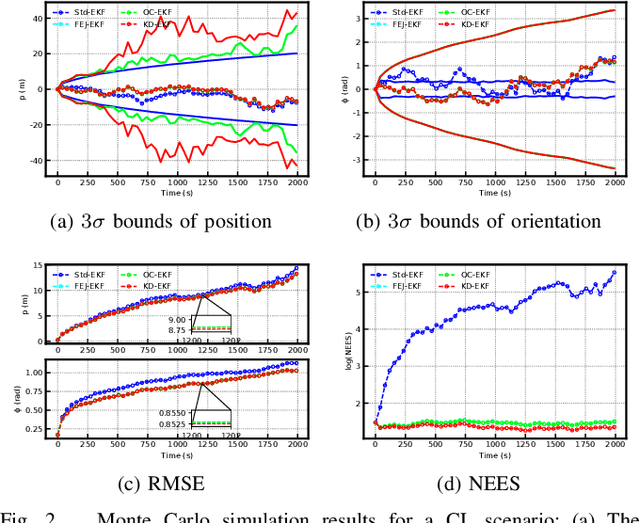
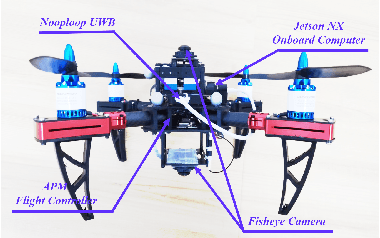

This paper investigates the consistency problem of EKF-based cooperative localization (CL) from the perspective of Kalman decomposition, which decomposes the observable and unobservable states and allows treating them individually. The factors causing the dimension reduction of the unobservable subspace, termed error discrepancy items, are explicitly isolated and identified in the state propagation and measurement Jacobians for the first time. We prove that the error discrepancy items lead to the global orientation being erroneously observable, which in turn causes the state estimation to be inconsistent. A CL algorithm, called Kalman decomposition-based EKF (KD-EKF), is proposed to improve consistency. The key idea is to perform state estimation using the Kalman observable canonical form in the transformed coordinates. By annihilating the error discrepancy items, proper observability properties are guaranteed. More importantly, the modified state propagation and measurement Jacobians are exactly equivalent to linearizing the nonlinear CL system at current best state estimates. Consequently, the inconsistency caused by the erroneous dimension reduction of the unobservable subspace is completely eliminated. The KD-EKF CL algorithm has been extensively verified in both Monte Carlo simulations and real-world experiments and shown to achieve better performance than state-of-the-art algorithms in terms of accuracy and consistency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge