Clustering multi-way data: a novel algebraic approach
Paper and Code
Feb 22, 2015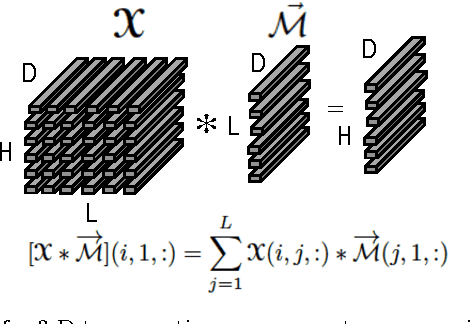
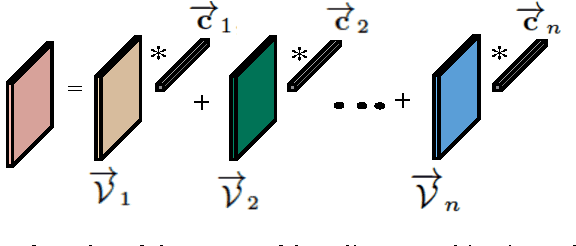
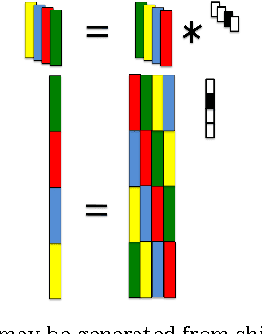

In this paper, we develop a method for unsupervised clustering of two-way (matrix) data by combining two recent innovations from different fields: the Sparse Subspace Clustering (SSC) algorithm [10], which groups points coming from a union of subspaces into their respective subspaces, and the t-product [18], which was introduced to provide a matrix-like multiplication for third order tensors. Our algorithm is analogous to SSC in that an "affinity" between different data points is built using a sparse self-representation of the data. Unlike SSC, we employ the t-product in the self-representation. This allows us more flexibility in modeling; infact, SSC is a special case of our method. When using the t-product, three-way arrays are treated as matrices whose elements (scalars) are n-tuples or tubes. Convolutions take the place of scalar multiplication. This framework allows us to embed the 2-D data into a vector-space-like structure called a free module over a commutative ring. These free modules retain many properties of complex inner-product spaces, and we leverage that to provide theoretical guarantees on our algorithm. We show that compared to vector-space counterparts, SSmC achieves higher accuracy and better able to cluster data with less preprocessing in some image clustering problems. In particular we show the performance of the proposed method on Weizmann face database, the Extended Yale B Face database and the MNIST handwritten digits database.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge