Multilinear Subspace Clustering

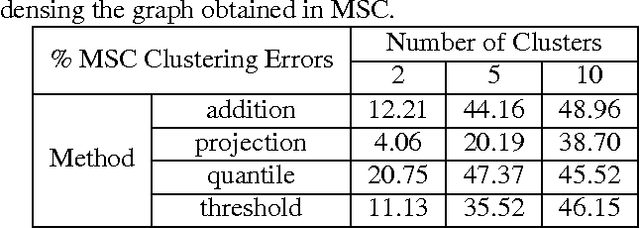
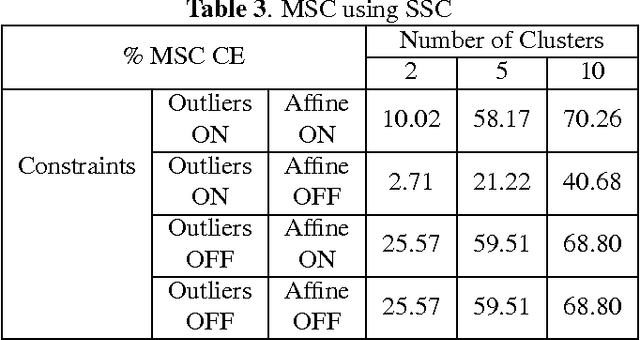
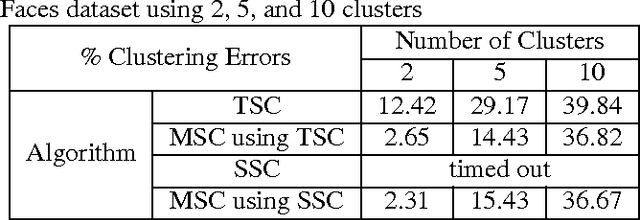
In this paper we present a new model and an algorithm for unsupervised clustering of 2-D data such as images. We assume that the data comes from a union of multilinear subspaces (UOMS) model, which is a specific structured case of the much studied union of subspaces (UOS) model. For segmentation under this model, we develop Multilinear Subspace Clustering (MSC) algorithm and evaluate its performance on the YaleB and Olivietti image data sets. We show that MSC is highly competitive with existing algorithms employing the UOS model in terms of clustering performance while enjoying improvement in computational complexity.

Group-Invariant Subspace Clustering

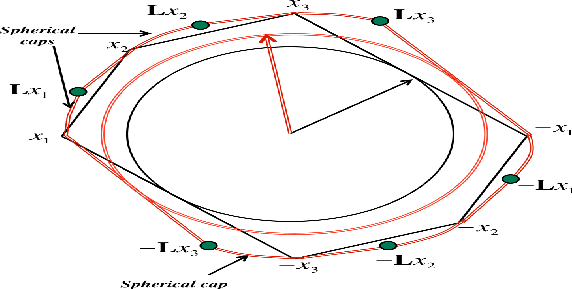
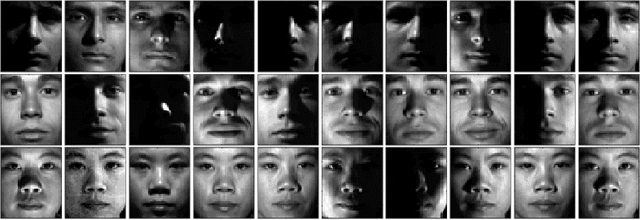
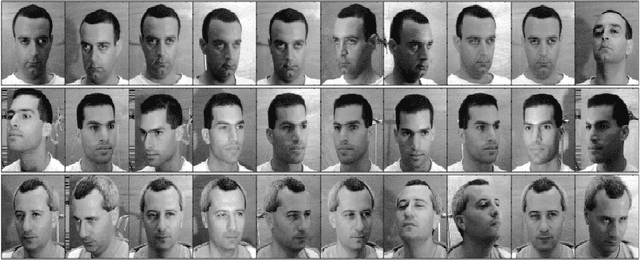
In this paper we consider the problem of group invariant subspace clustering where the data is assumed to come from a union of group-invariant subspaces of a vector space, i.e. subspaces which are invariant with respect to action of a given group. Algebraically, such group-invariant subspaces are also referred to as submodules. Similar to the well known Sparse Subspace Clustering approach where the data is assumed to come from a union of subspaces, we analyze an algorithm which, following a recent work [1], we refer to as Sparse Sub-module Clustering (SSmC). The method is based on finding group-sparse self-representation of data points. In this paper we primarily derive general conditions under which such a group-invariant subspace identification is possible. In particular we extend the geometric analysis in [2] and in the process we identify a related problem in geometric functional analysis.

Clustering multi-way data: a novel algebraic approach

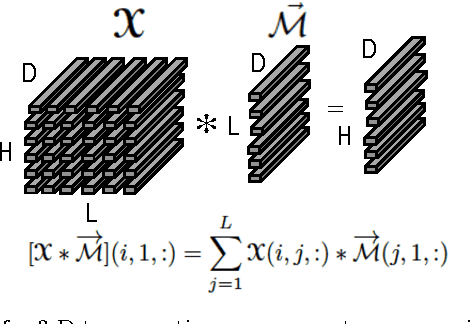
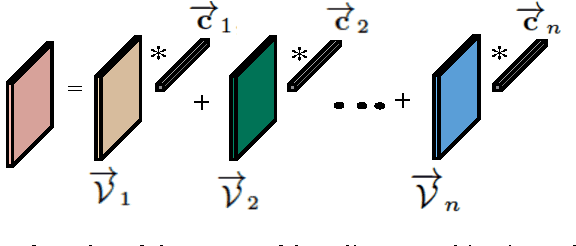
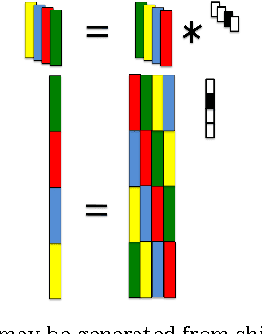
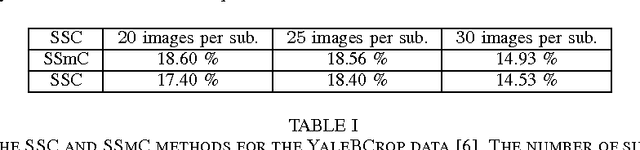
In this paper, we develop a method for unsupervised clustering of two-way (matrix) data by combining two recent innovations from different fields: the Sparse Subspace Clustering (SSC) algorithm [10], which groups points coming from a union of subspaces into their respective subspaces, and the t-product [18], which was introduced to provide a matrix-like multiplication for third order tensors. Our algorithm is analogous to SSC in that an "affinity" between different data points is built using a sparse self-representation of the data. Unlike SSC, we employ the t-product in the self-representation. This allows us more flexibility in modeling; infact, SSC is a special case of our method. When using the t-product, three-way arrays are treated as matrices whose elements (scalars) are n-tuples or tubes. Convolutions take the place of scalar multiplication. This framework allows us to embed the 2-D data into a vector-space-like structure called a free module over a commutative ring. These free modules retain many properties of complex inner-product spaces, and we leverage that to provide theoretical guarantees on our algorithm. We show that compared to vector-space counterparts, SSmC achieves higher accuracy and better able to cluster data with less preprocessing in some image clustering problems. In particular we show the performance of the proposed method on Weizmann face database, the Extended Yale B Face database and the MNIST handwritten digits database.