Image classification using local tensor singular value decompositions
Paper and Code
Jun 29, 2017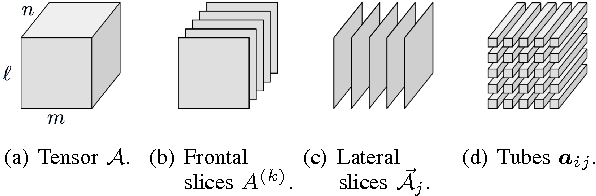
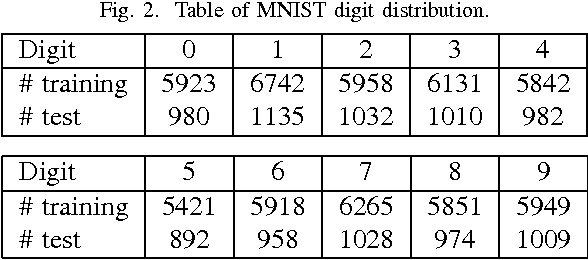
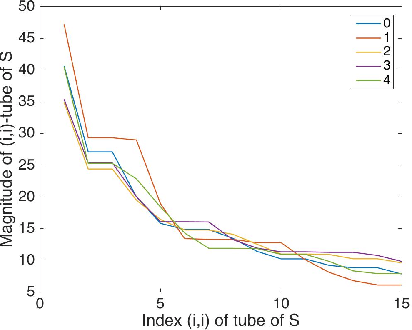
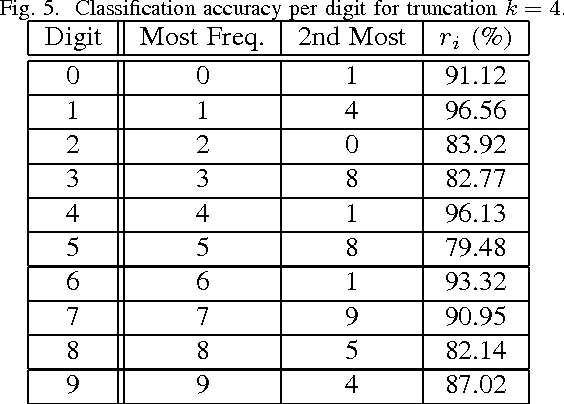
From linear classifiers to neural networks, image classification has been a widely explored topic in mathematics, and many algorithms have proven to be effective classifiers. However, the most accurate classifiers typically have significantly high storage costs, or require complicated procedures that may be computationally expensive. We present a novel (nonlinear) classification approach using truncation of local tensor singular value decompositions (tSVD) that robustly offers accurate results, while maintaining manageable storage costs. Our approach takes advantage of the optimality of the representation under the tensor algebra described to determine to which class an image belongs. We extend our approach to a method that can determine specific pairwise match scores, which could be useful in, for example, object recognition problems where pose/position are different. We demonstrate the promise of our new techniques on the MNIST data set.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge